温度计 Thermo

标准数独基础上，每条温度计上的数字从圆圈开始增大。

Classic rules applied, additionally, numbers increase from bulb on each thermometer.

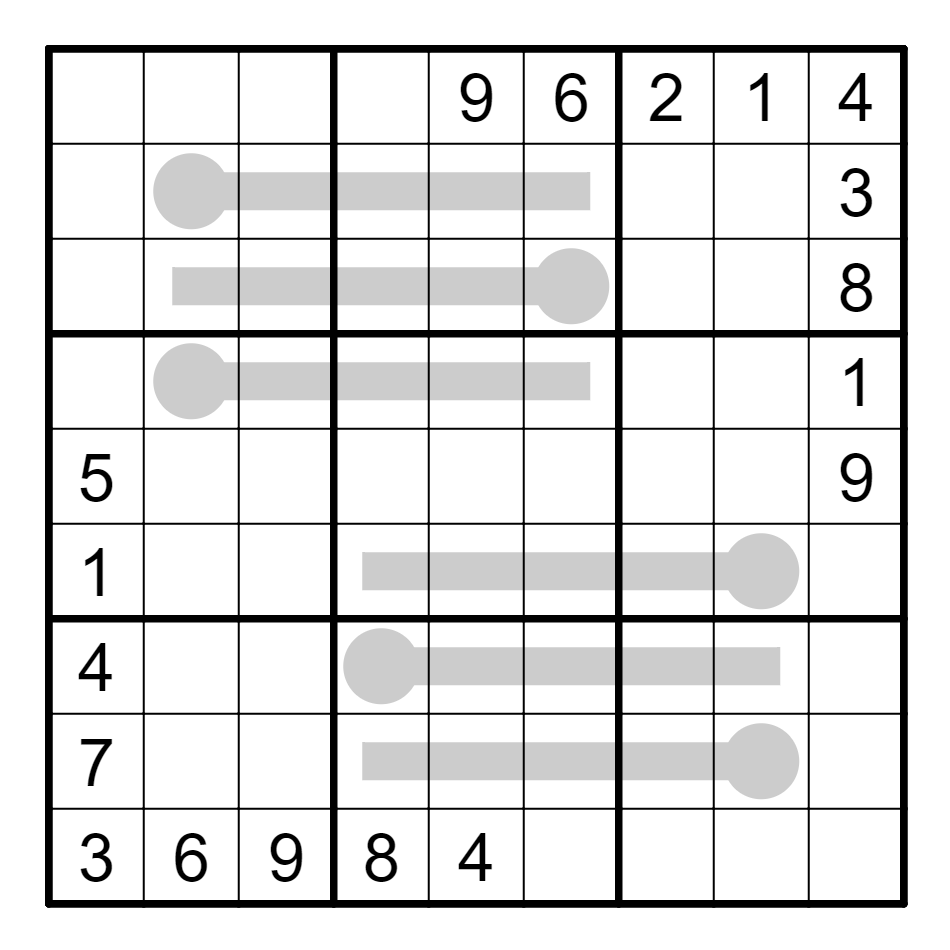
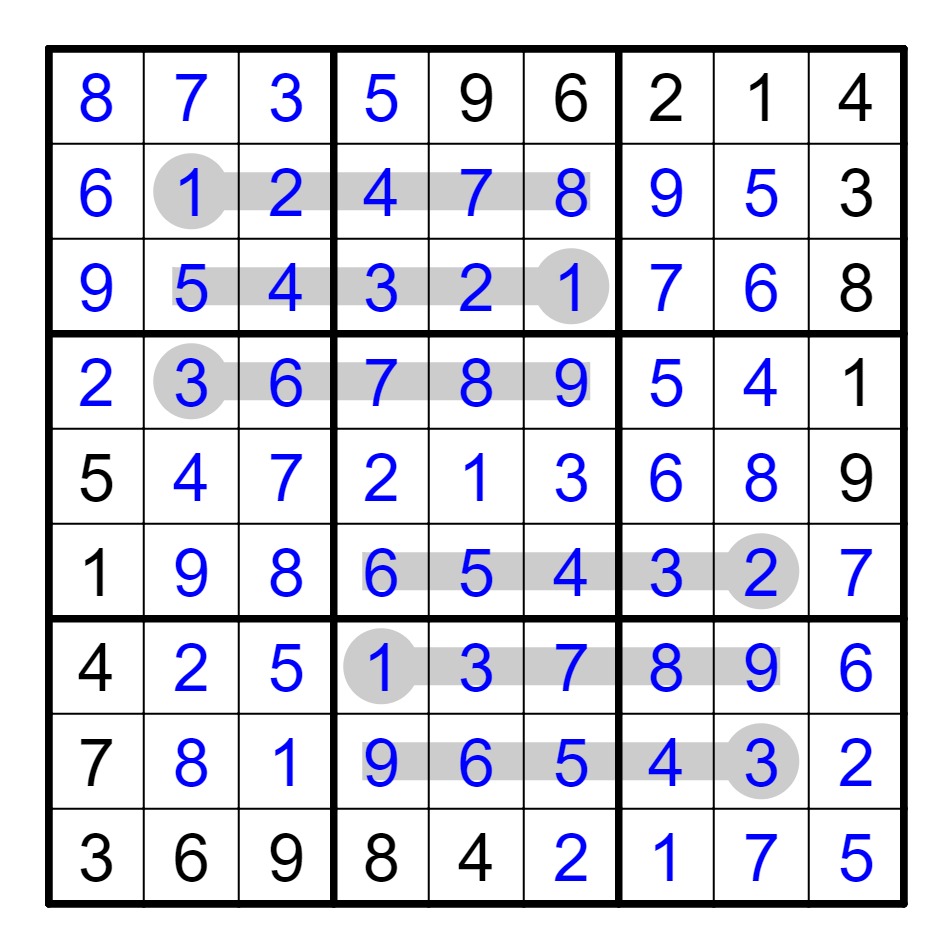
*这个案例是我的作品，但被菲律宾亚锦赛剽窃了。

赛事频率 极高

*中小学生赛事U10及以上年龄组高可能出现；全国性无组别赛事、洲际及世界级赛事内必定出现。

*较小的校内/市内比赛可能不会有。

*目前可考的资料中，早在2010年以前就在正式赛事内出现。

易错点 等差数列

温度计上的数字不一定构成等差数列，例如12345和12359都符合条件。一些资料中将规则描述为[温度计上数字从圆圈起严格增大]。

要点① 长温度计上的候选数取值

在N阶题目中，如果温度计线长为M，则无已知数的条件下，每格内有{N-M+1}个（记为K个）候选数。从圆圈格起，第一格的候选数为[1~K]，第A格的候选数为[A~(A+K-1)]。

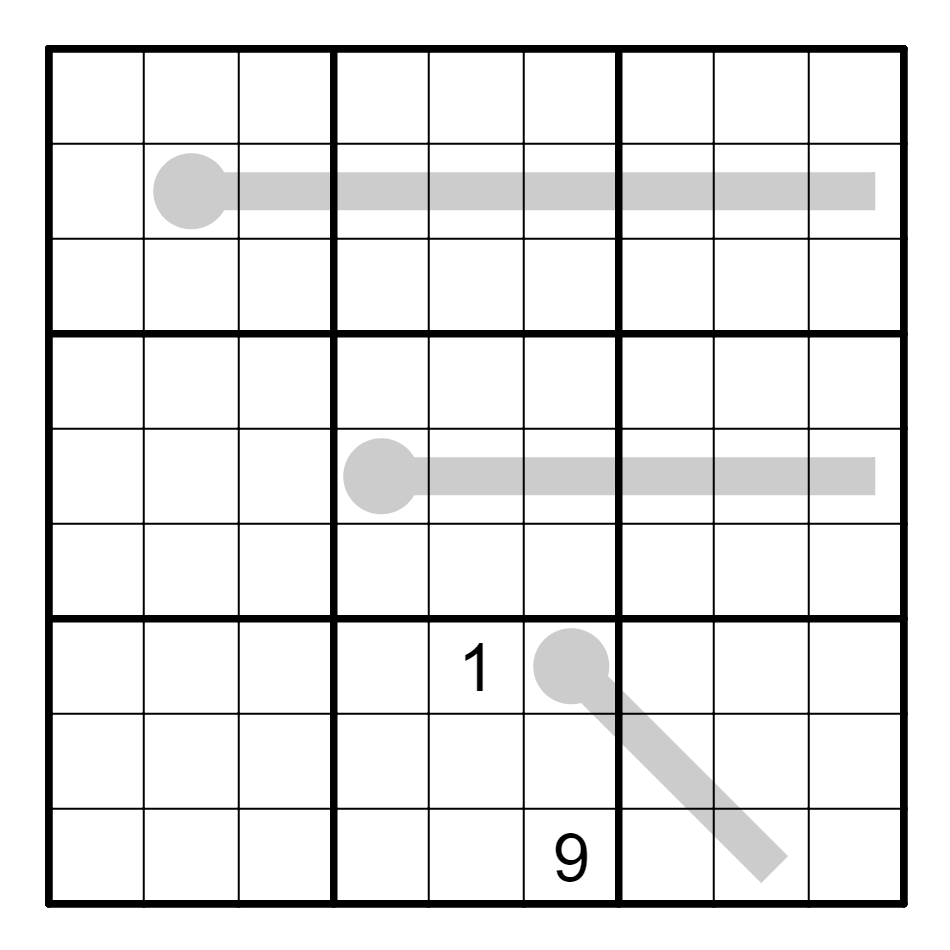
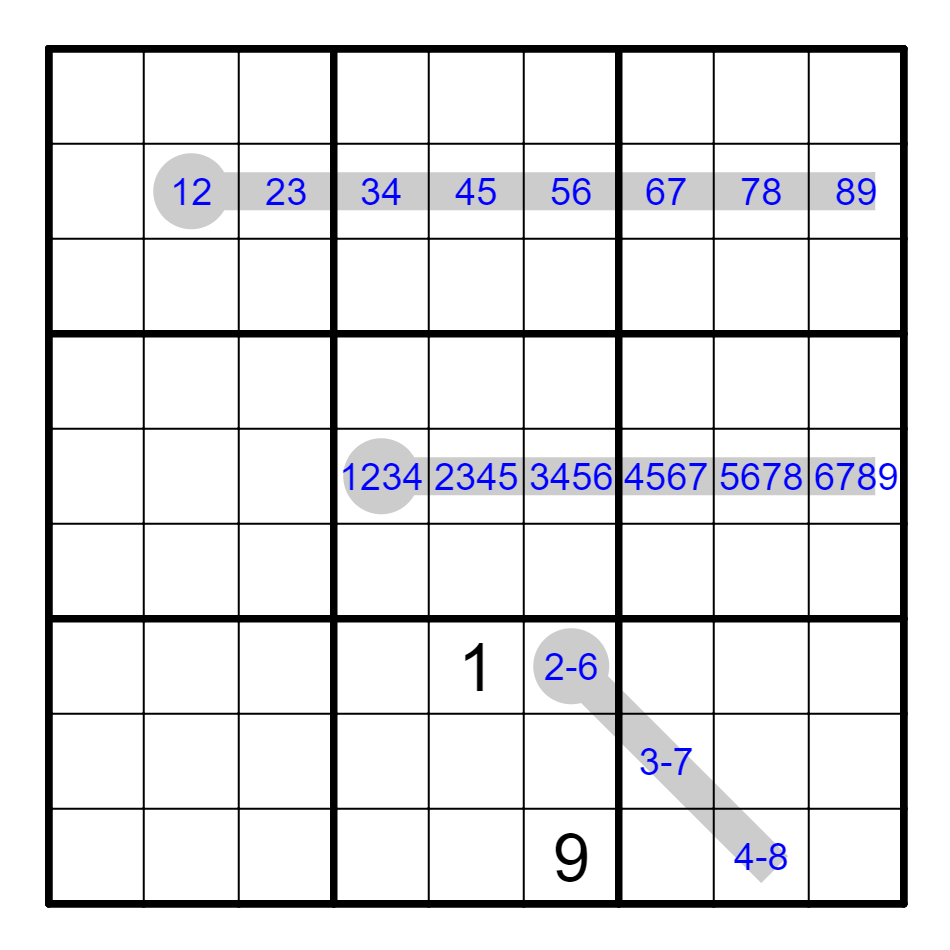
此外，温度计上的数会受到已知数字的影响，进而缩减范围。如果某格的范围从[A~B]缩减为[(A+i)~(B-j)]，那么远离圆圈的另一格会由[C~D]变为[(C+i)~D]，靠近圆圈的另一格会由[E~F]变为[E~(F+j)]。这样的范围变化很可能引起出数，并且带来新的一轮范围变化。

定义① 线长

在一条温度计上，从起点起，至其中某个终点结束，所经过的格数称为温度计的线长。

例如下图中，从起点S起，到达A的温度计线长为5，到达B的温度计线长为3。对于处于温度计岔路口的单元格（例如下图C格），讨论其候选数情况时，应当应对不同的分岔线进行分类讨论，并取其候选数集的交集。

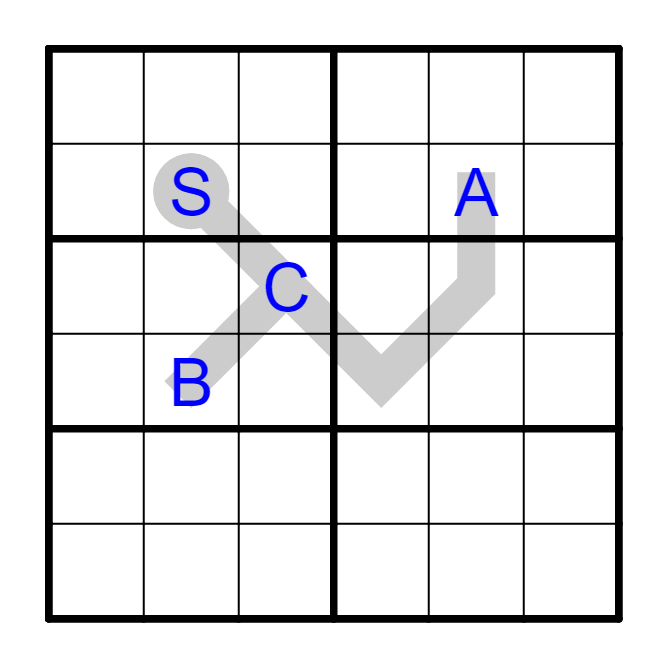
一般而言，如无已知数字影响，候选数集的交集等于最长线在此格的候选数集，即C的取值范围等于S-A线中C的取值范围[2~3]。但是如若S-B线被已知数影响，例如B不等于4、5、6，则此时会发现C格无法取到3，这时会有C=2。

实际上的情况会比理论上复杂更多，有时候S-B线也会受到更复杂的候选数影响。

要点② 特殊数字定位

在不等号数独的案例中，我们提到定位数字1和数字N的方法，在温度计数独中同样适用，甚至更为直观。

很显然的是，数字1不能在任何温度计的直线部分上（可能在圆球或白格）。因此，单纯定位数字1，会比不等号数独中同样的操作，在观察上更为容易。

观察数字N（N是阶数，也是盘面内最大的数字）也比较容易，以六阶数独为例，最大的数字6只能在白格，或是温度计的末尾。

如果一个行/列/宫内有且仅有一格符合条件，那么目标数字一定在这一格中。

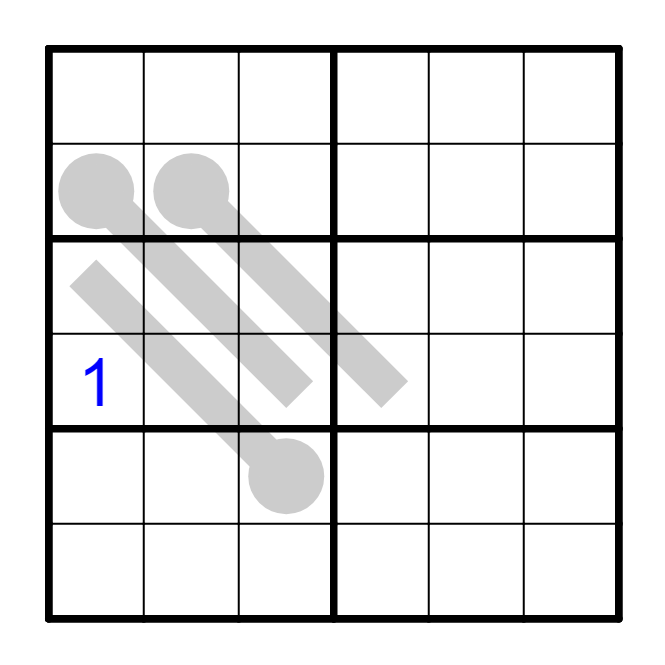
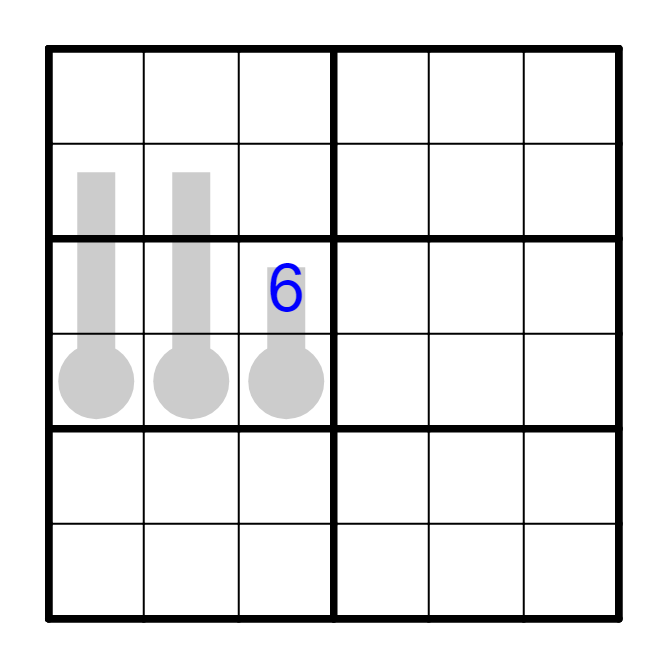
我们得到了一个数字以后，可以用其排除其余的区域，减少观察目标的范围，然后确定其余区域内该数字的位置。

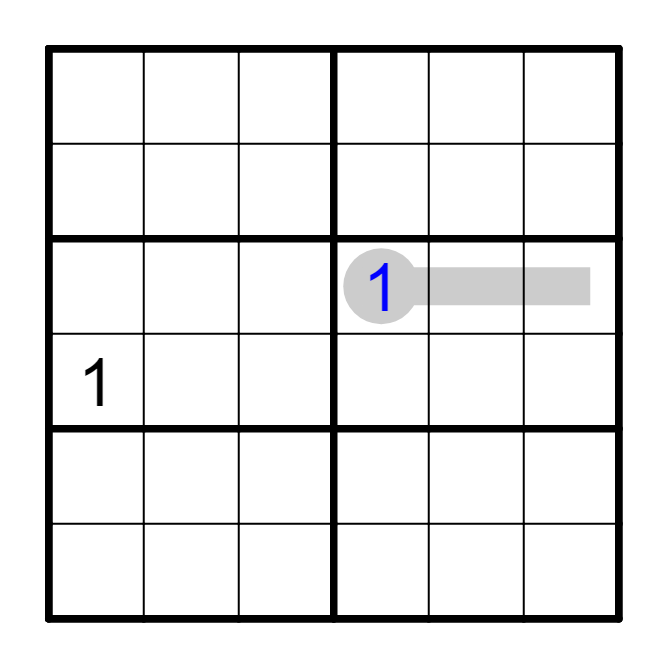
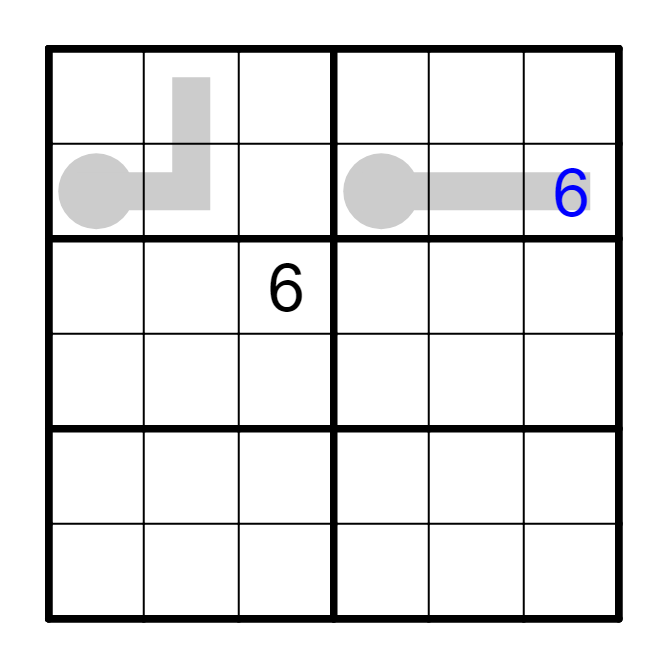
要点③ 长温度计候选数互斥

（待施工）

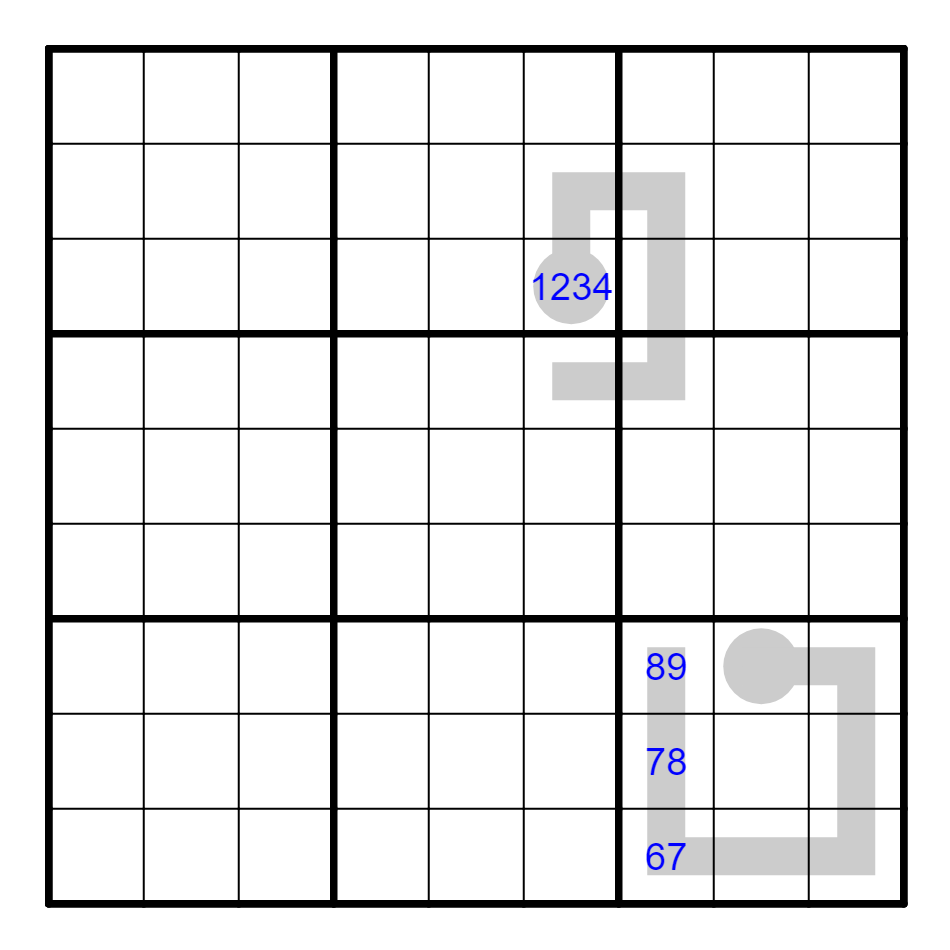
要点④ 不完全额外区域与等价性

一般而言，线上的数字都是不完全额外区域。因此，可以利用额外区域的一些性质，例如三角删减。

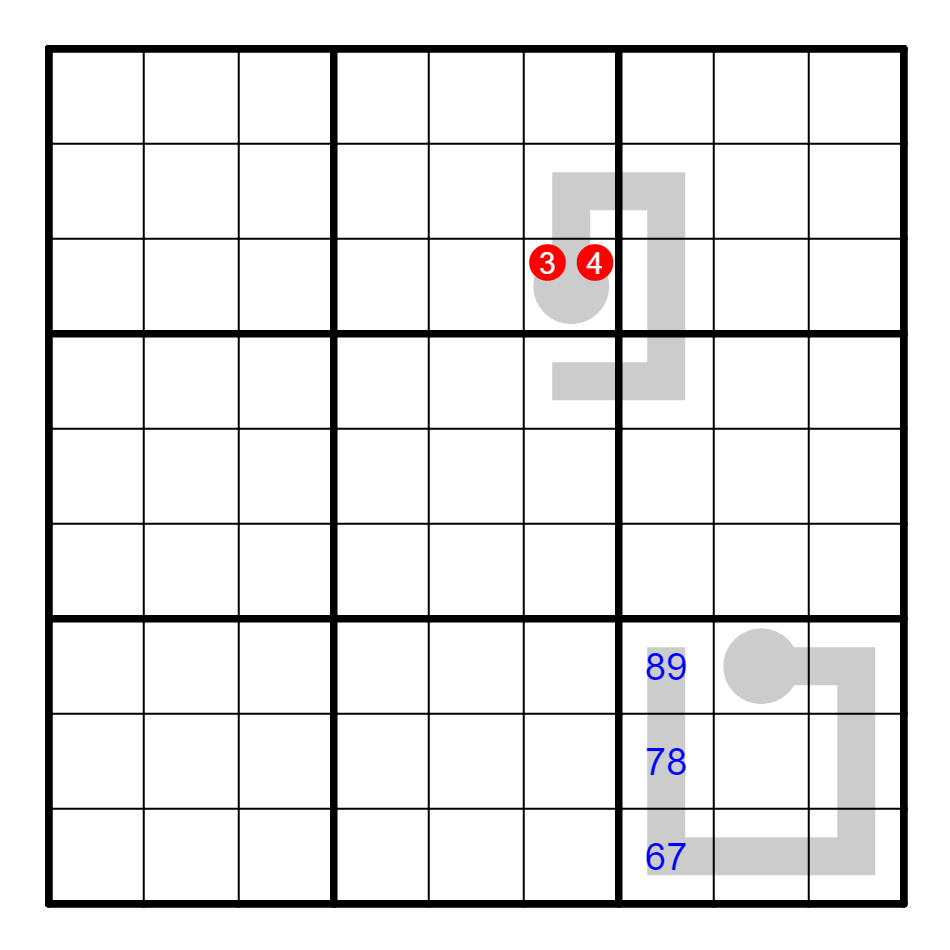
例① 通过3的三角删减，删除C4的3。

也可以同样利用4的三角删减，删掉C4的4，然而因为候选结构的关系，温度计上的候选数并不包含4。

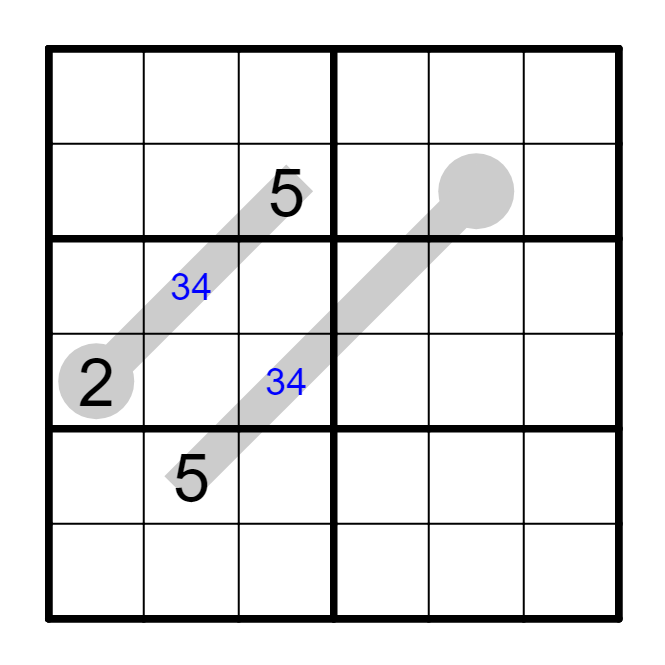
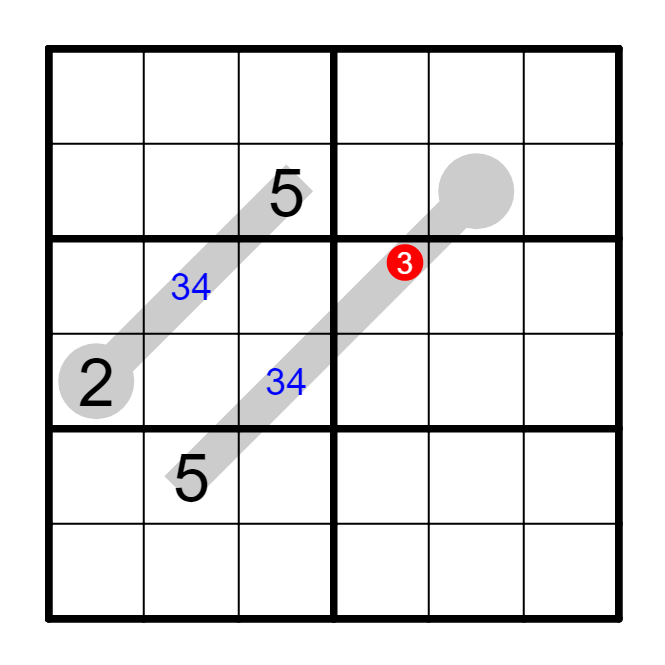
练习

① 在9x9 温度计中，一条没有分岔的温度计占据了7个单元格。其中从圆圈开始的第三、第四、第五格不是5，第二格可能是______，第七格可能是______。

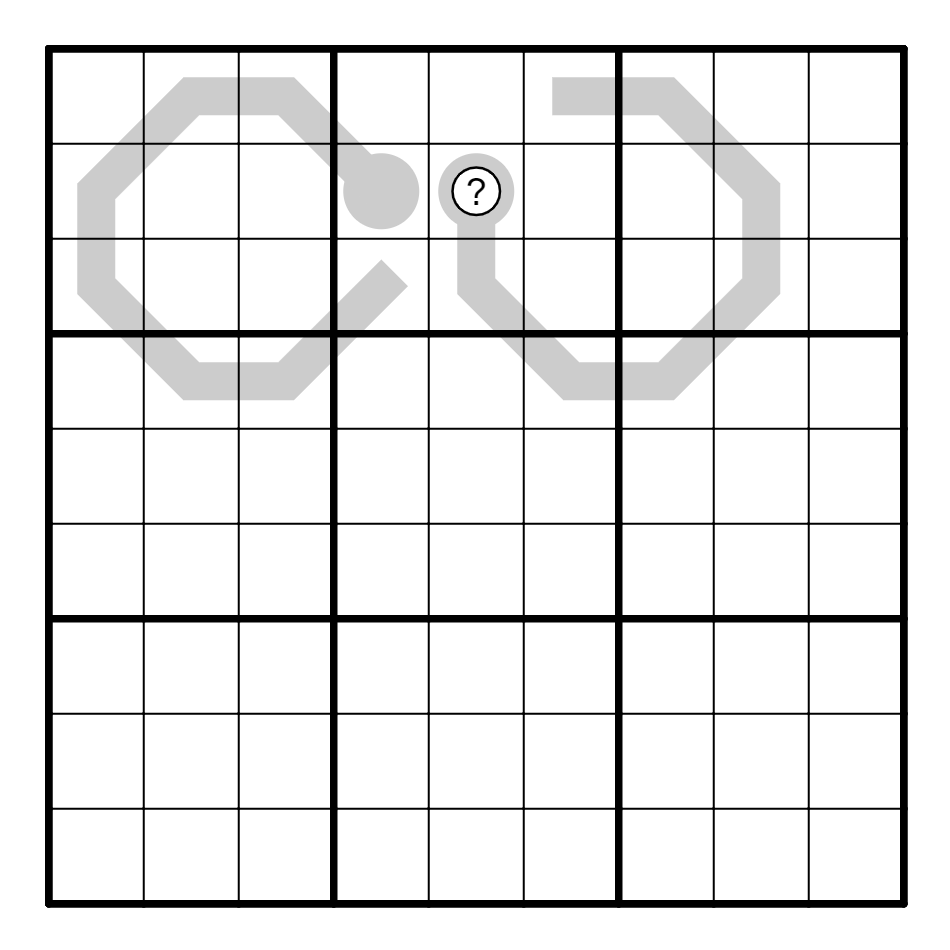
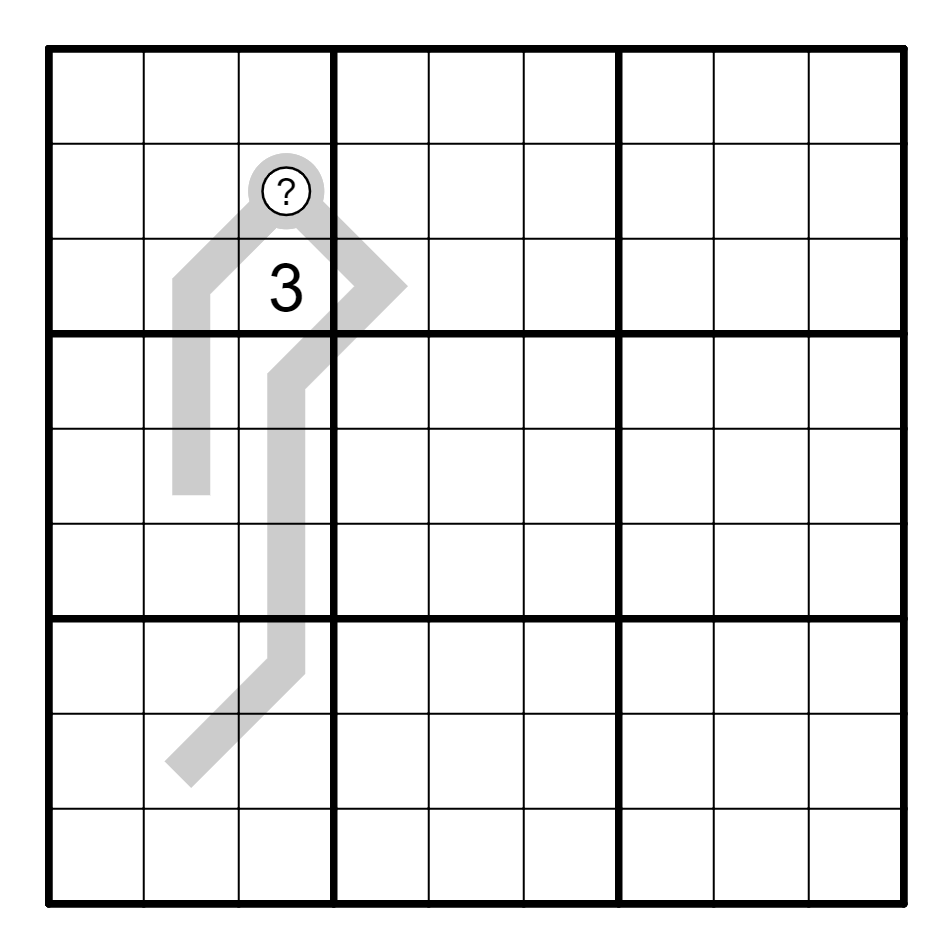
② 找出问号格的取值。

③ 思考：

(1) 温度计数独和不等号数独有哪些异同点？

(2) 为什么说一般而言温度计每条线上都是不完全额外区域？

答案

① 2或3; 8或9.

② B5=2; B3=1; C1=6.

③ (1) 温度计本质上是一种广义上的不等号数独，但是有斜向的温度计对应斜向的不等号，是基础的不等号所难以表达的；不等号数独也可以转化为温度计数独，但是不等号较多容易造成温度计重叠及覆盖。

(2) 每条线上数字增大，所以每个数字都不相同；温度计上数字有顺序，如果线长等于阶数，那么我们可以直接写出所有的数字（此时构成完全额外区域，但是没有任何意义）；而如果温度计的线长不等于阶数，那么此时构成不完全额外区域。