杀手 Killer
标准数独基础上,每个提示是框内数字之和,且框内数字不重复。
Classic rules applied, additionally, the little clue is the sum of each cage, and numbers cannot repeat in each cage either.
赛事频率 极高
国内外各类型赛事(除中小学比赛极低年龄组)几乎必有题型。
要点① 21/45法则 The rule of 21/45
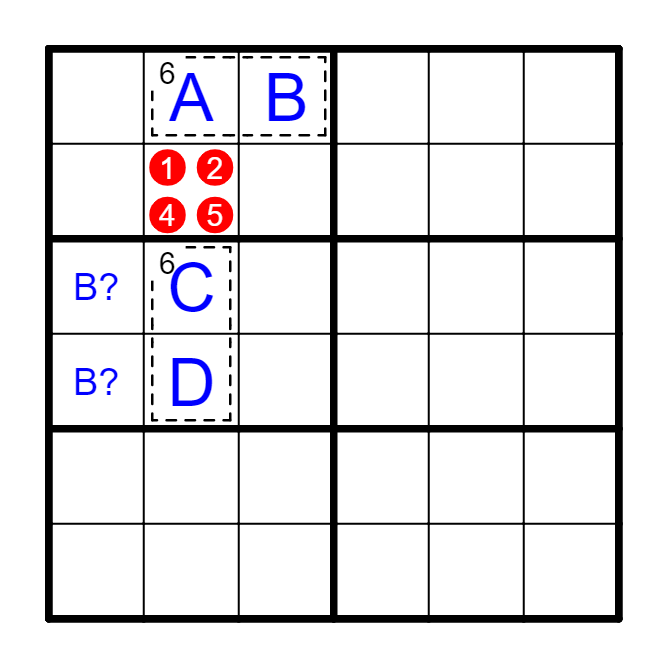
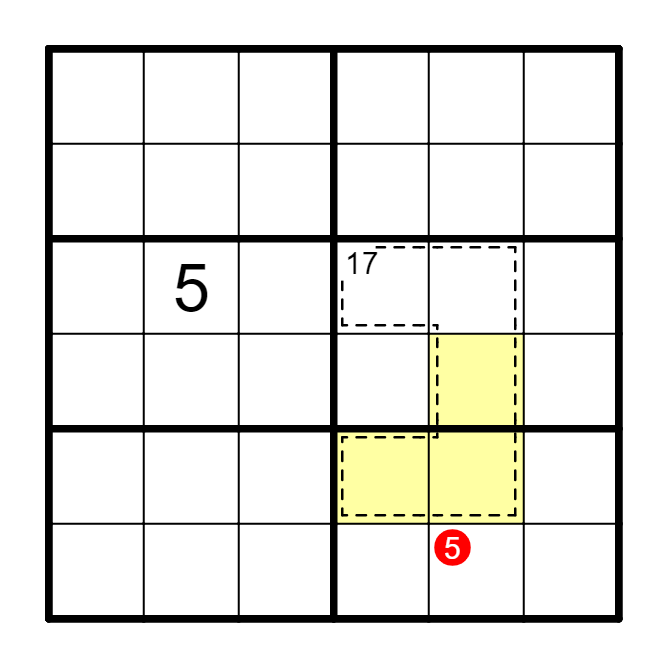
在六阶杀手之中,每一行/列/宫内含有1~6,它们之和是21,记为S=21(九阶题目里是45)。所以我们可以对虚线框求和,并与21/45进行比对。
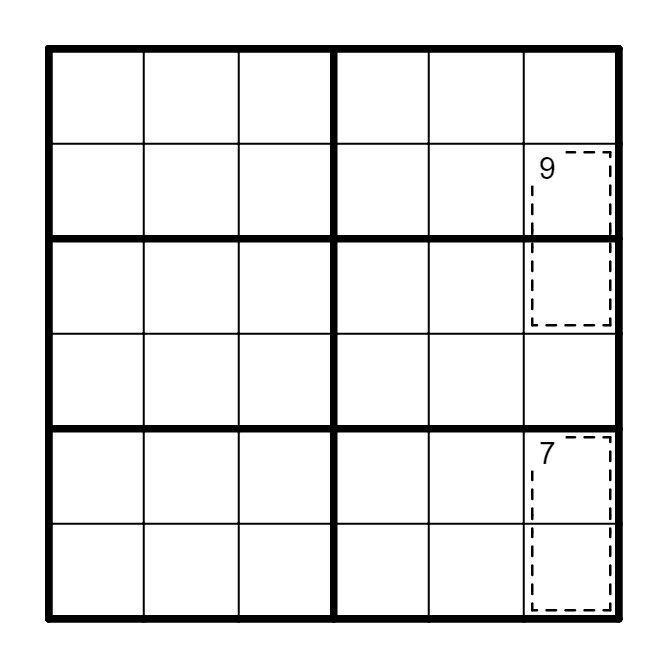
例 第一宫和C3的数字之和是26,C3=26-21=5。
例 虚线框数字之和是38,但前两行的数字之和是42,B6=42-38=4。
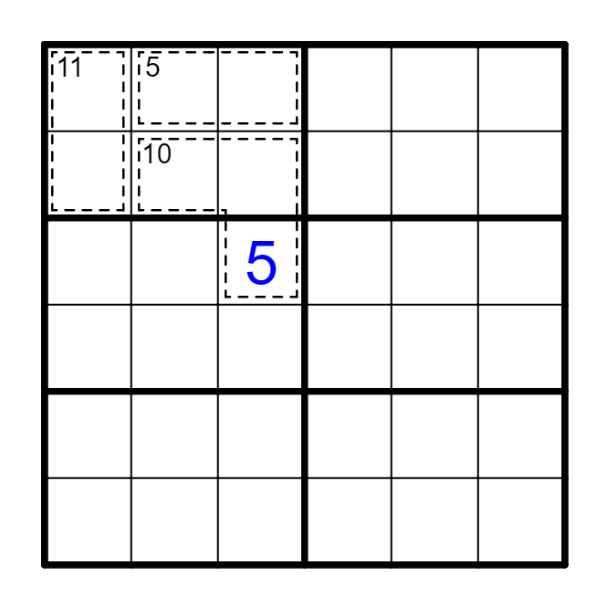
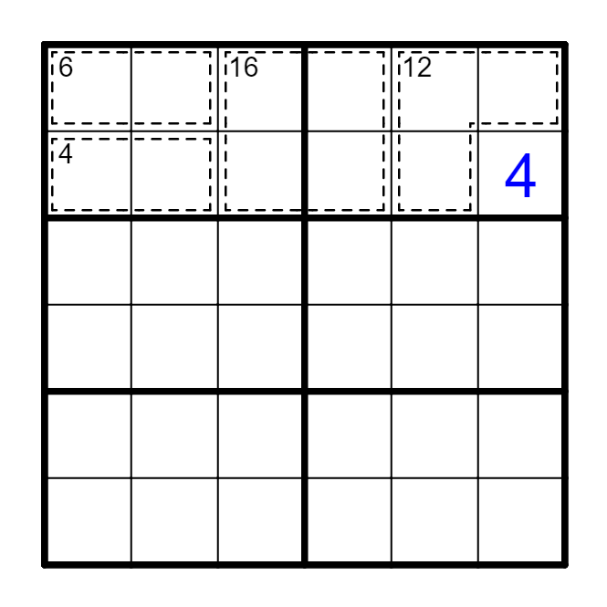
例 虚线框和为21→B3=C1;D6-E4=5→D6=6,E4=1。
例 粉色+黄色=7,粉色=1,黄色是123的组合才能满足条件。
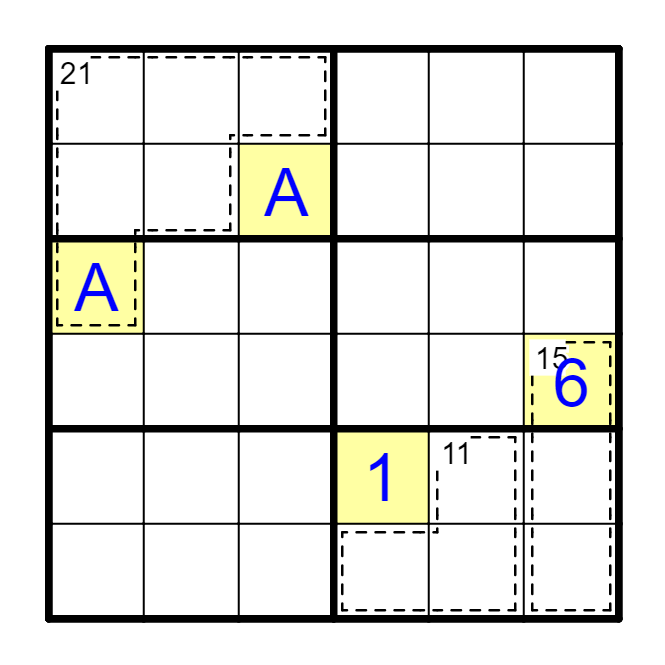
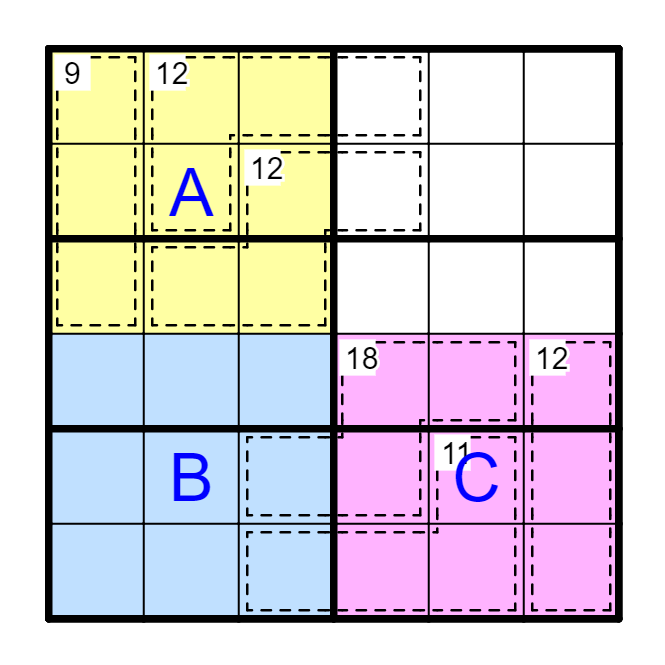
要点② 互补
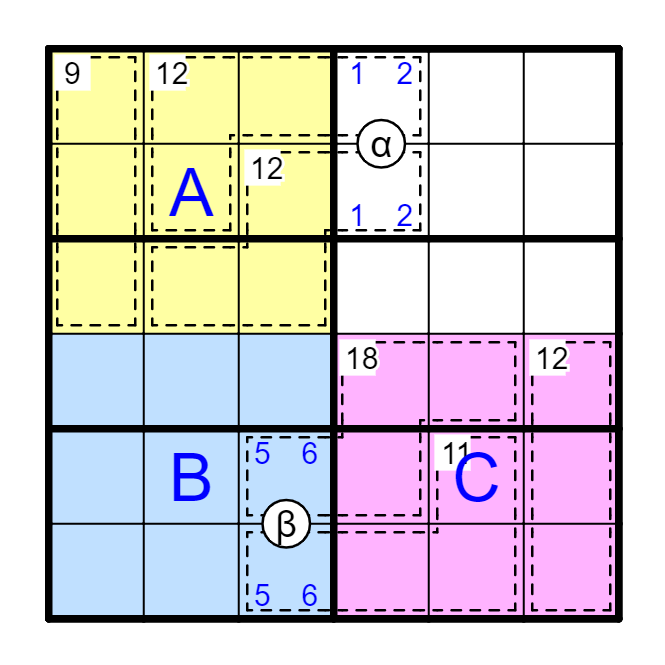
例 观察涂色的A,B,C区,及α区(A4+D4)、β区(E3+F3)。
A区+B区=B区+C区=21x3 → A区之和=C区之和。
β区-α区=8,考虑极限情况得β区是5+6,α区是1+2方可满足。
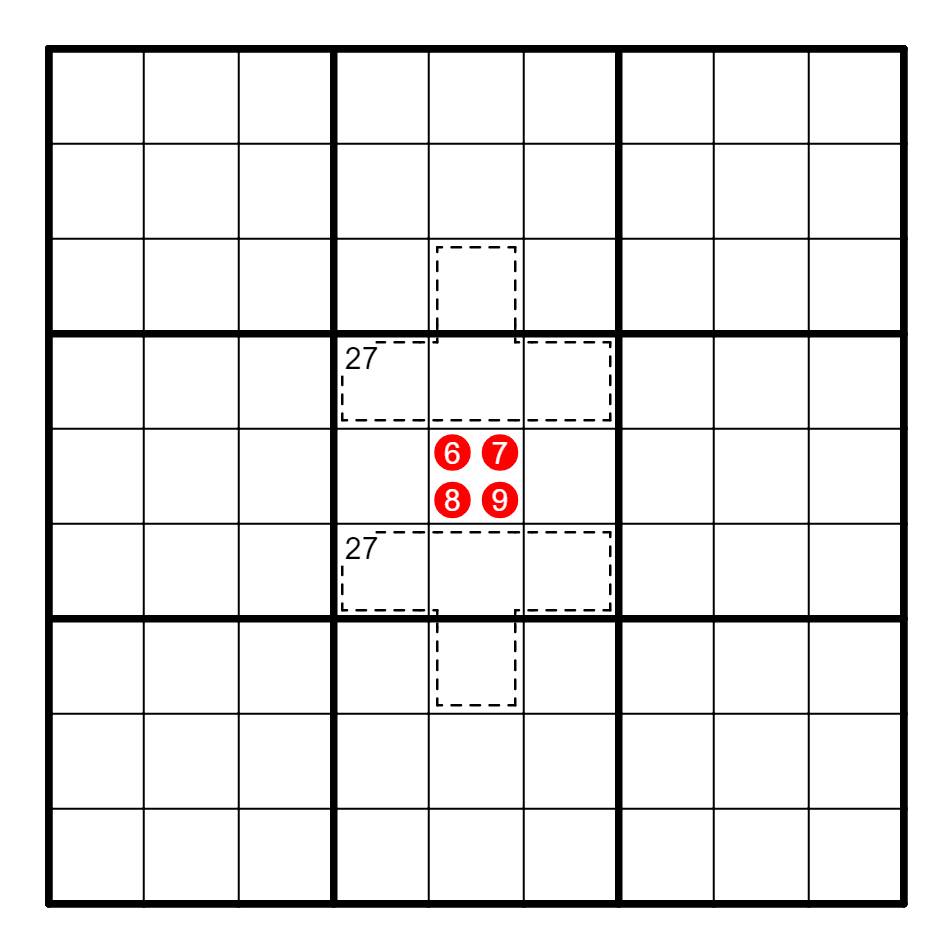
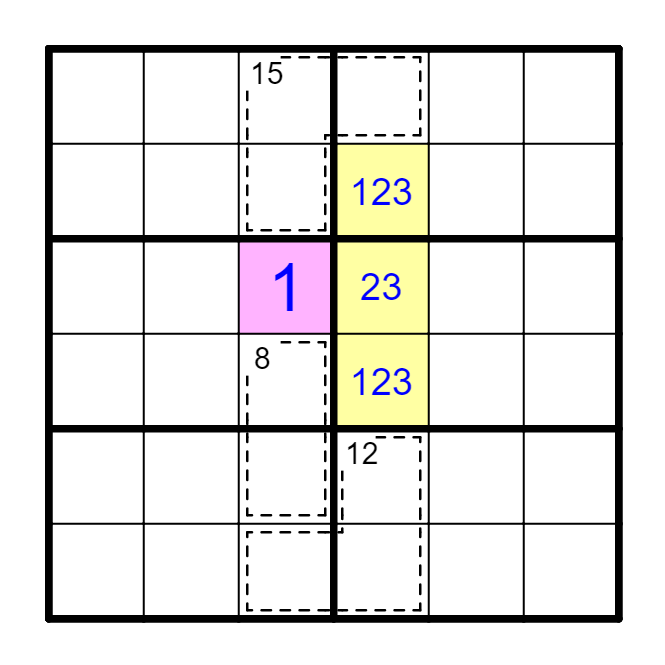
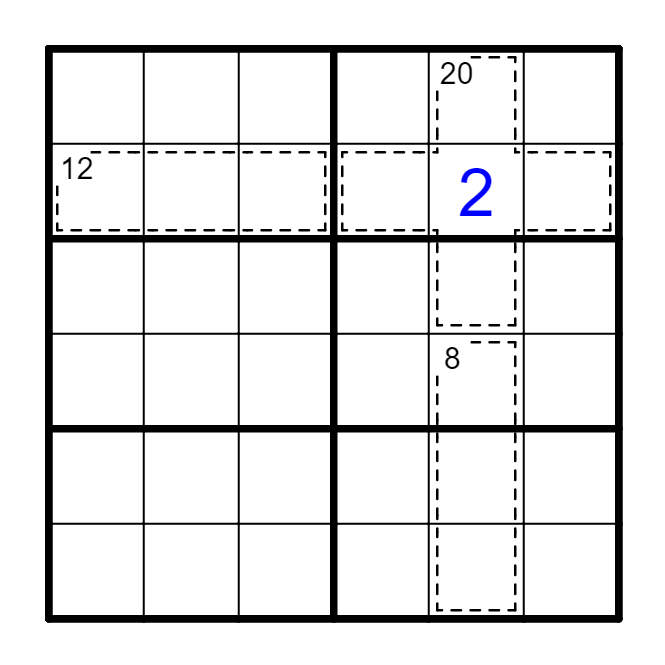
例 框内和=40,二列+五宫=42,B5=2。*此法别名容斥定理。
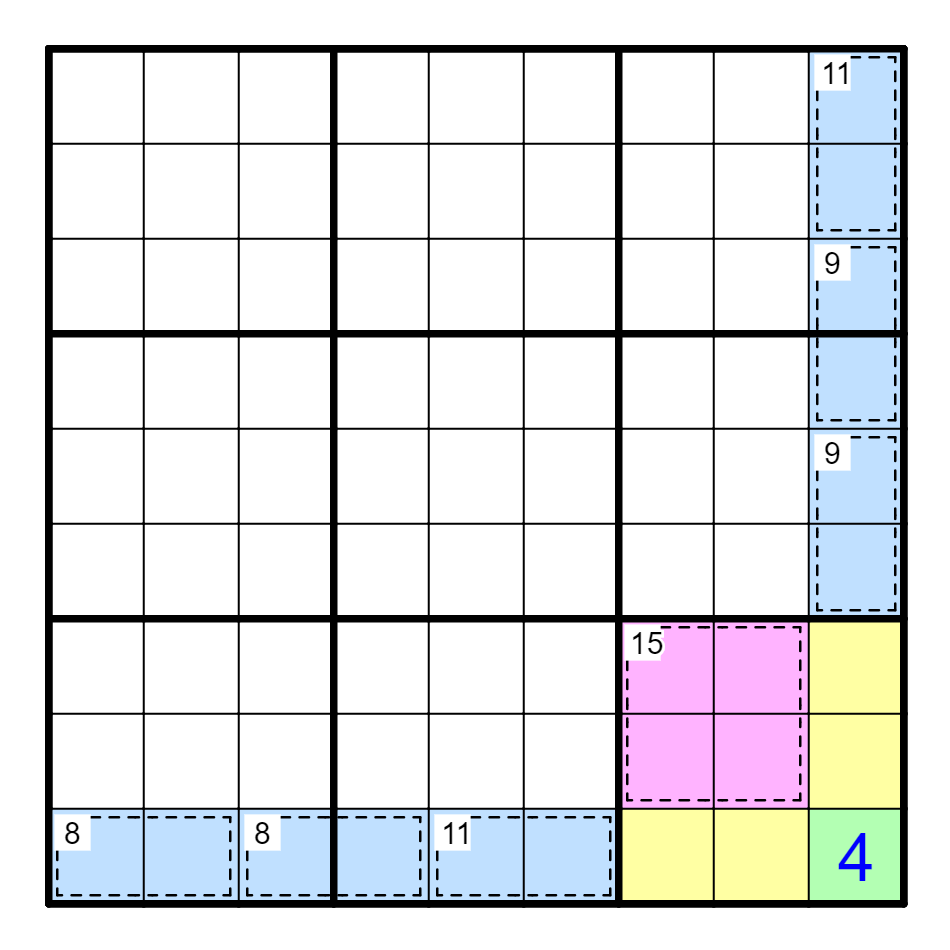
例 I9=45+粉色-蓝色=4。
补充说明 尾数
我们可以仅计算尾数,但我们不建议在需要计算多个数字的和/差时使用。
在要点②的例4中,B5=42-(12+20+8)=2-(2+0+8)=2。
练习1
① 四阶数独中,S是多少?
② 解答问号格 Find out the ?cell.
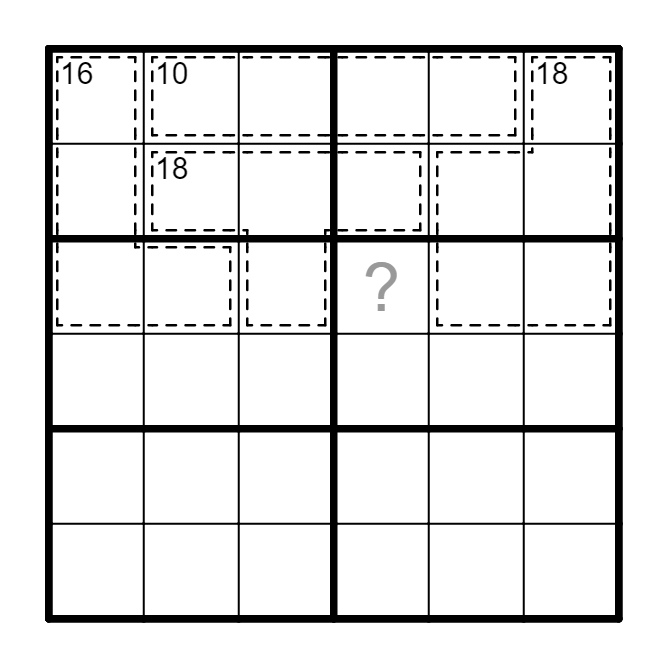
答案1
① 10 ② C4=1.
要点③ 和的分析
每个虚线框内数字不重复,但是一些框内可能有唯一的数字拆分。我们用A[B]表示数字A是B个数字之和。
例 结合框内已知数字。
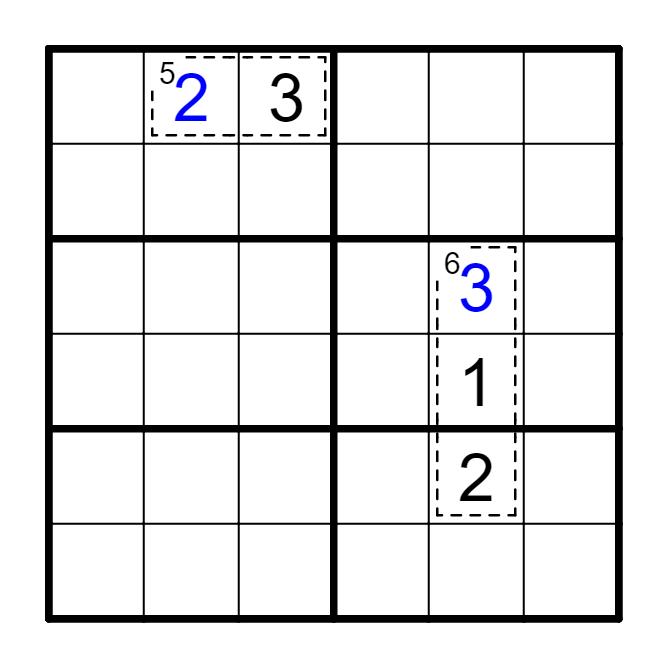
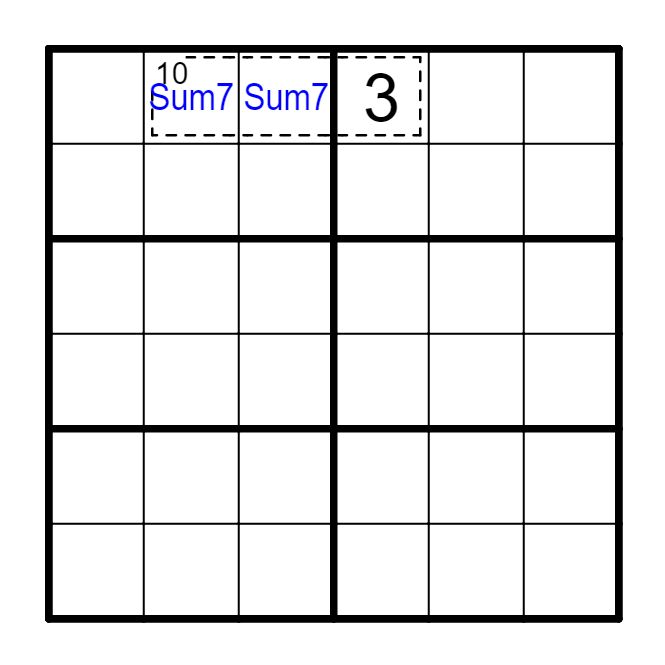
(1) 唯一拆分
以下组合为九阶题目中的唯一拆分,需要牢记。

(2) 双可能拆分
列举了九阶中部分双可能拆分。解题时需要判定拆分的属性。

一般地,以下三种情况可能推进解题进程:
① 框内所有数字不能为某个数 → 断定拆分。
② 框内有某个数的区块 → 断定拆分。
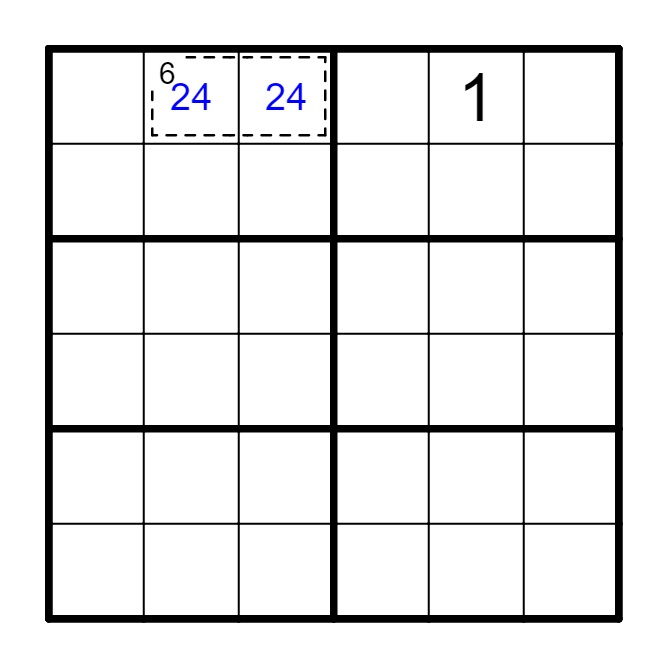
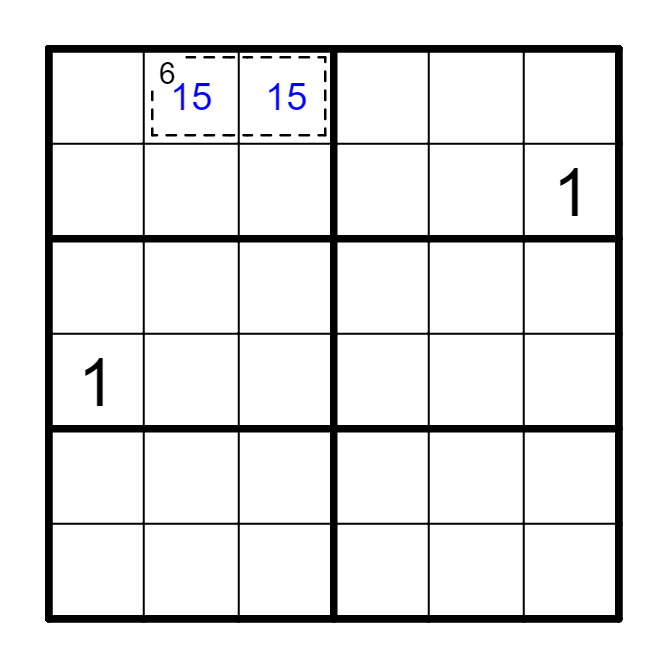
③ 结合候选数进行删减。
(a) 拆分abc...k所有单元格同时影响的一个单元格,其候选是abc...k的子集时,该拆分不成立。
(b) 如果拆分是abc....k时,其中p个候选数只能处于q(q<p)个单元格中时,该拆分不成立。
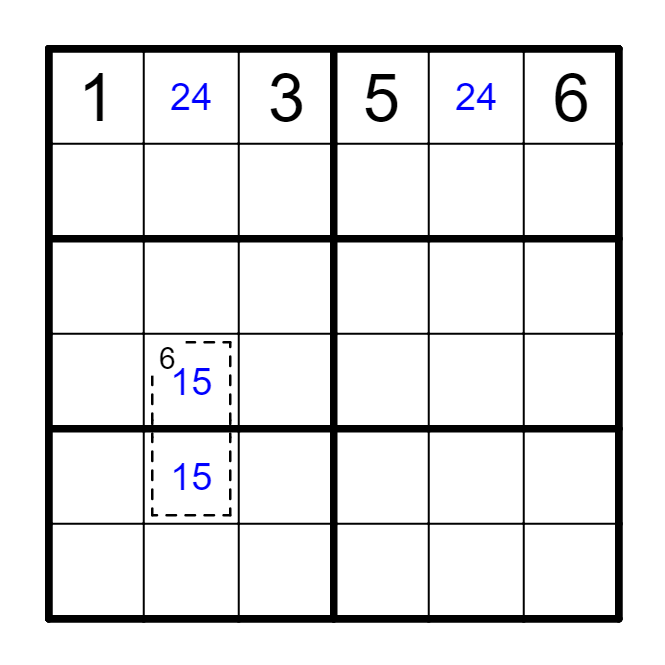

要点④ 必定包含、必不包含
如果一个组合有多种拆分,可以研究[无论哪一种拆分都包含]和[无论哪一种拆分都不包含]的情况。
下图是四个最常见的[必定包含]的案例。

必定存在的数字,可以在框内寻找其隐性唯一,或可以当作区块使用。

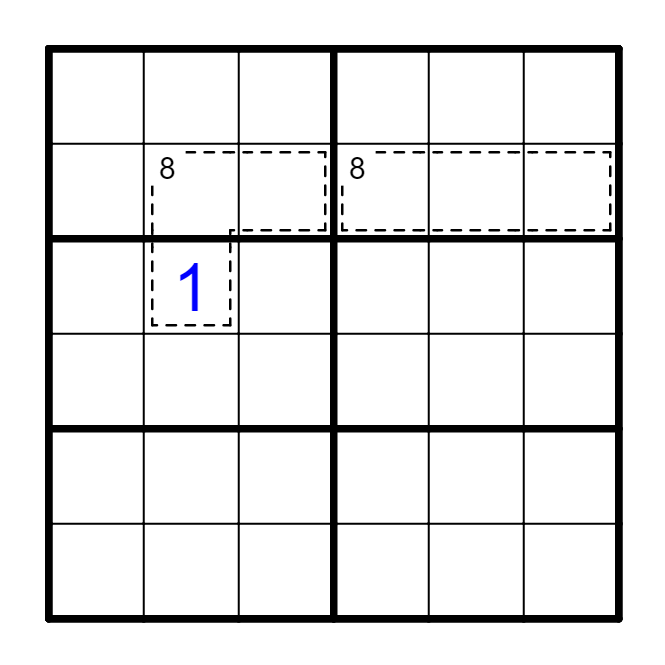
必定不存在的数字有如下情况:
(1) 2k[2]一定不包含k。
(2) A[M]=A1+A2+......AM,对于∀i∈{1~M},有:
A-A[M-1]max≤Ai≤A-A[M-1]min
例 8[3]=A1+A2+A3,A[2]min=1+2=3,Ai≤8-3=5.
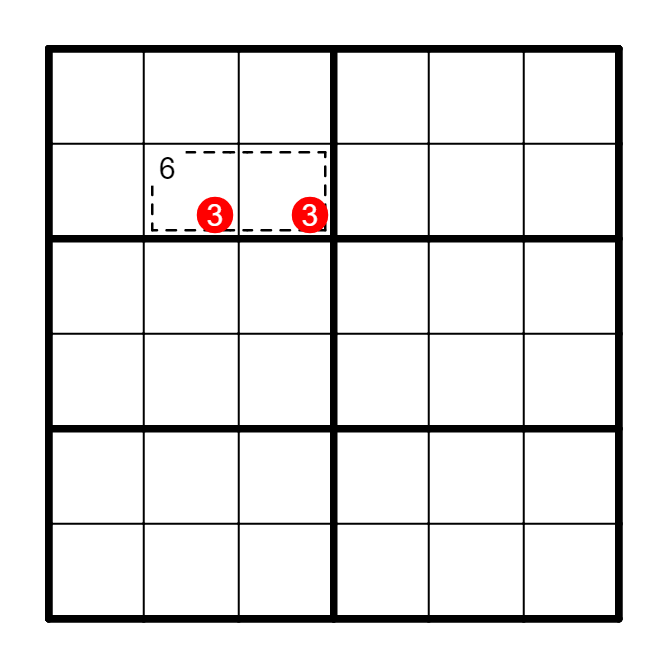

(3) 对于N阶题目中,每一行/列/宫内数字之和S,有S=A[K]+B[N-K].
即K个数字被包含,必定N-K个数字未被包含,可以对未被包含的格子之和做互补视角下的拆分。
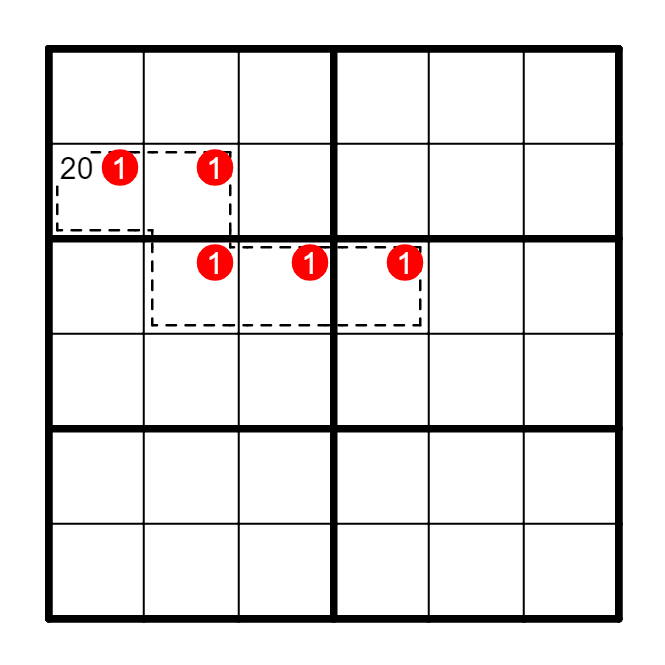
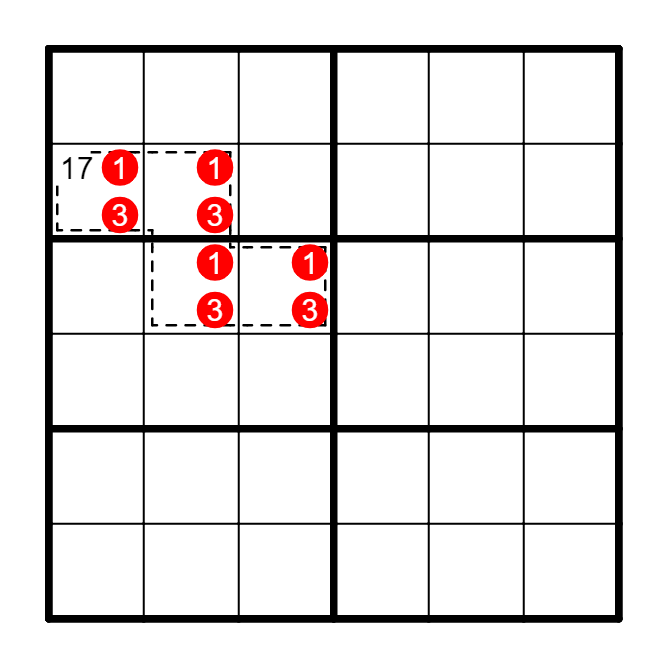
(4) 隐性唯一Hidden Singles
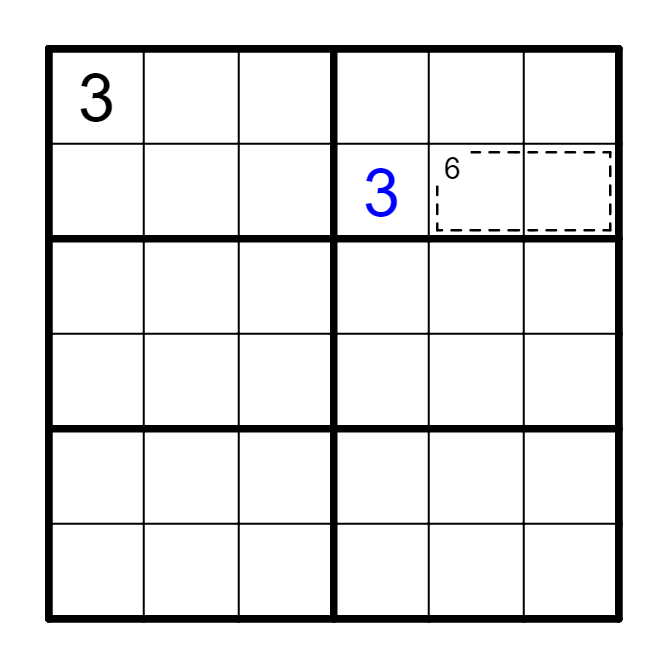
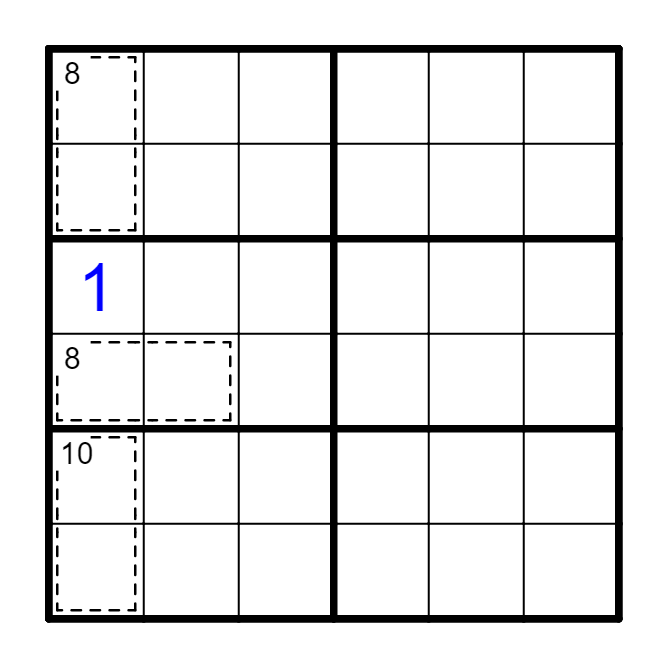
要点⑤ 组合互斥
如果同一个区域内部有两个框,我们可以合并它们作为一个大框进行处理,此时能更直观地观察组合互斥的情况。
例 5[2]+6[2]=11[4]=1235 → 5[2]=2+3,6[2]=1+4。
同理14[2]及15[2]互斥,14[2]=5+9,15[2]=7+8。
例 10[3]+11[3]=21[6]=123456, 10[3]=136/145/235;
10[2]+11[2]=21[4],但21[4]不是特殊组合,仅能用普通的组合互斥视角拆分。
都不含34的情况下10[2]=19/28,11[2]=29/56,显然11[2]≠29。


练习2
① 在N阶杀手中,无论N是几,12[2]不能包含______。
② 九阶杀手中,20[3]没有______,19[5]一定有______。
③ 六阶杀手中,13[4]一定有______。如果A[4]一定没有1,A可能是______。
④ 六阶杀手中,写下一定没有5,B≥3的所有A[B]组合。
⑤ 证明六阶杀手数独中,14[3]拆分唯一。
⑥ 解答问号格。
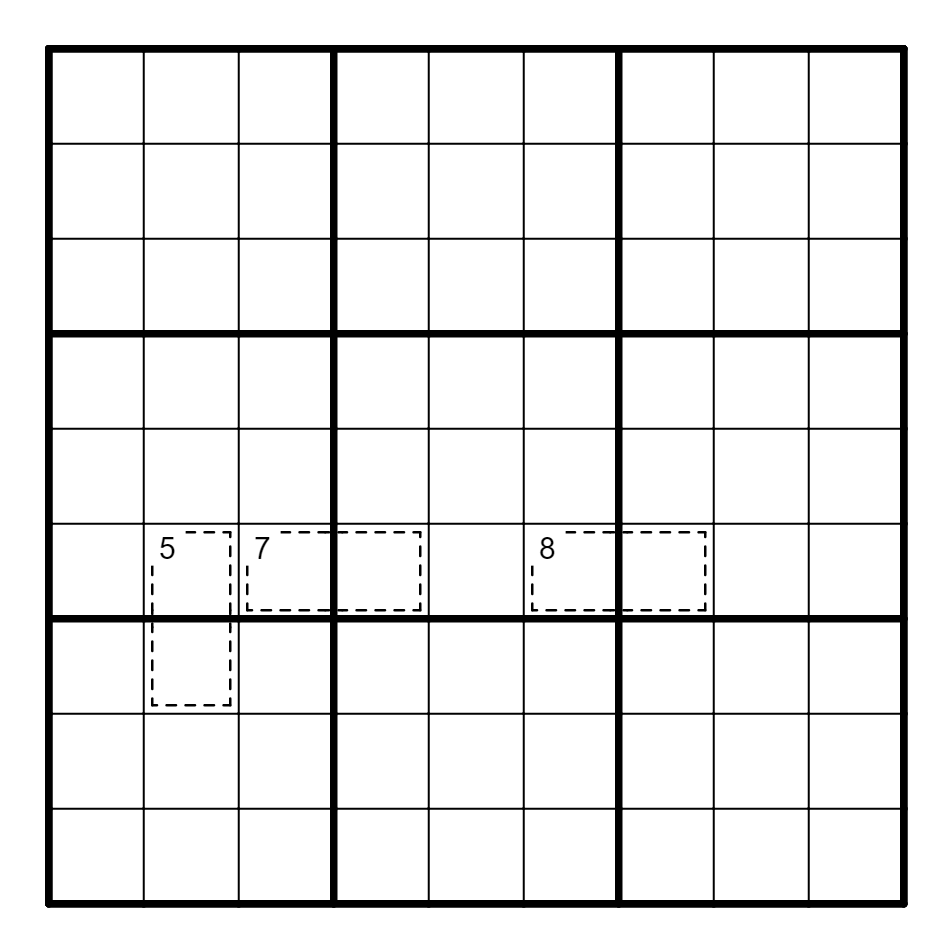
答案2
① 6 ② 1和2; 1 ③ 1; 17 或 18 ④ 6[3], 7[3], 10[4], 16[5]
⑤ 7[3]唯一拆分,14[3]=21-7[3]。
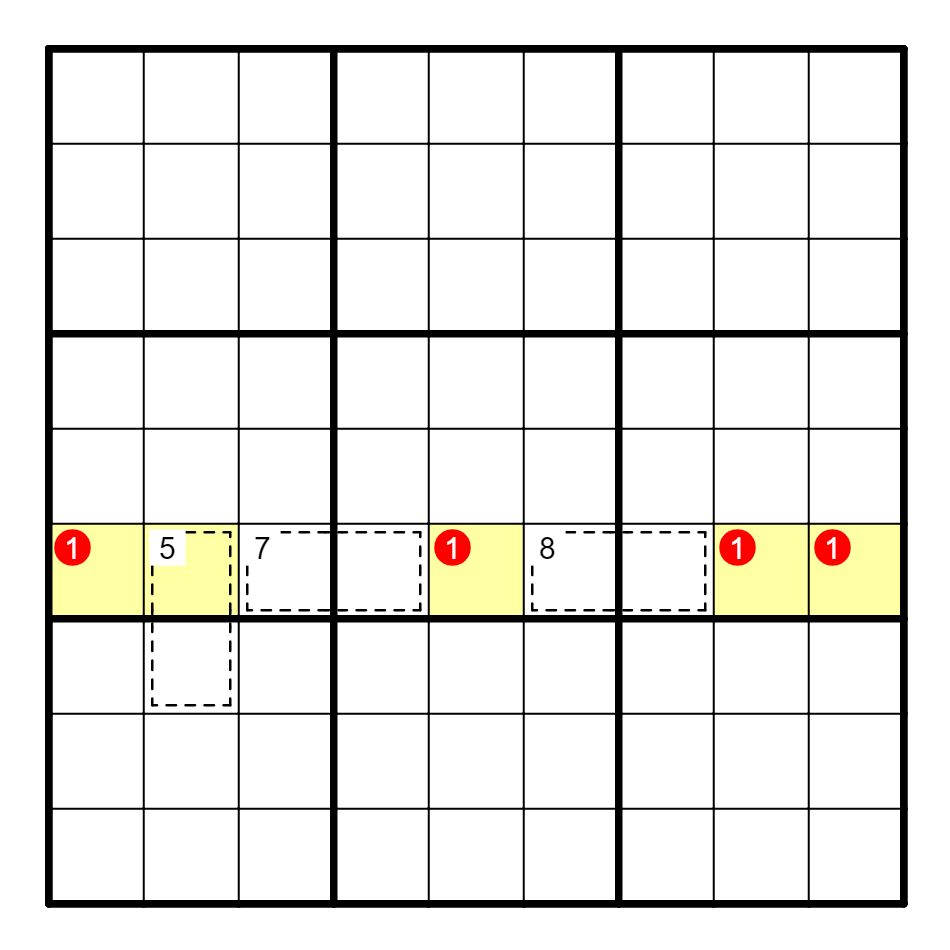
⑥ 如图所示。
黄色格之和是30,将30[5]视为1+29[4],29[4]=5789。
如果30[5]在F2以外的单元格有1,其余格至少是5,这时F2将没有数字可以填入。

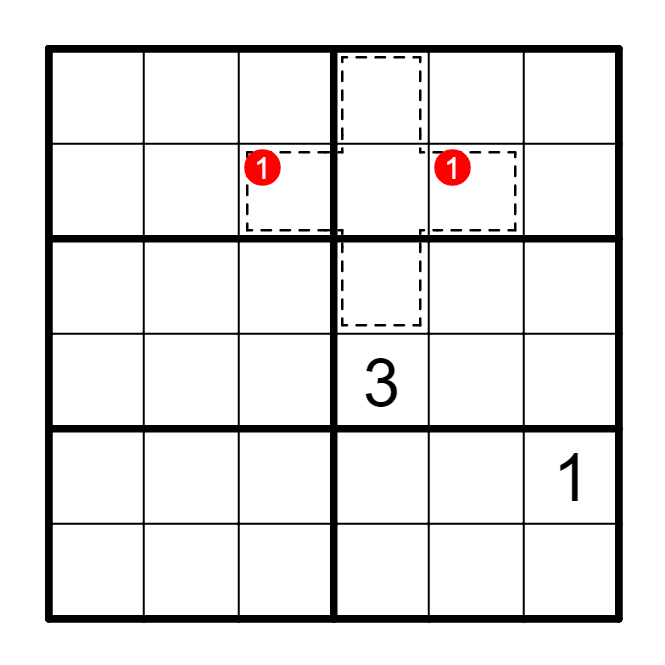
要点⑥ 框内不重复的使用
框内数字不重复,因此一些额外区域类数独的思路可以使用。
(1) 结合框内一定有某数,形成区块。
(2) 虚线框内区块形成的删减。
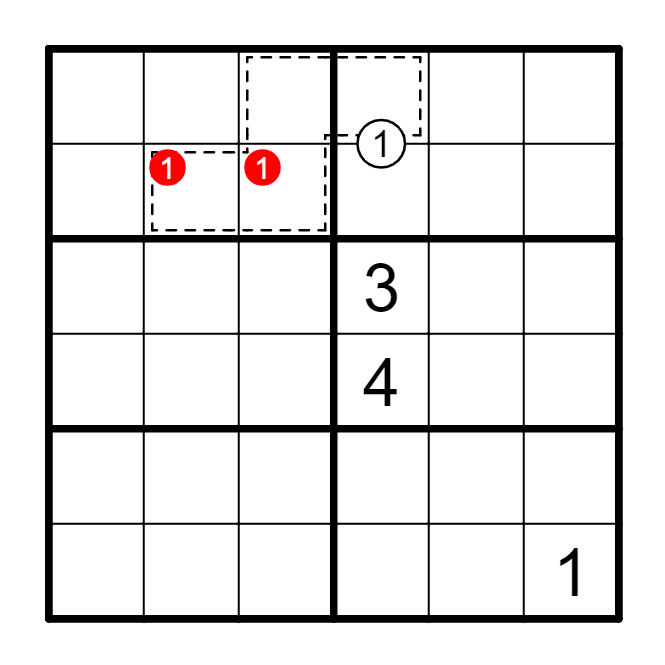
(3) 虚线框内组合区块。
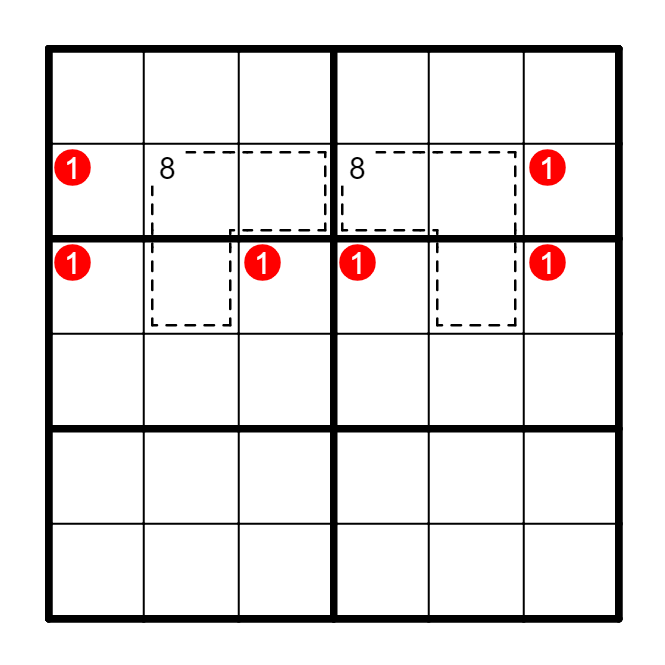
(4) 虚线框内数对组
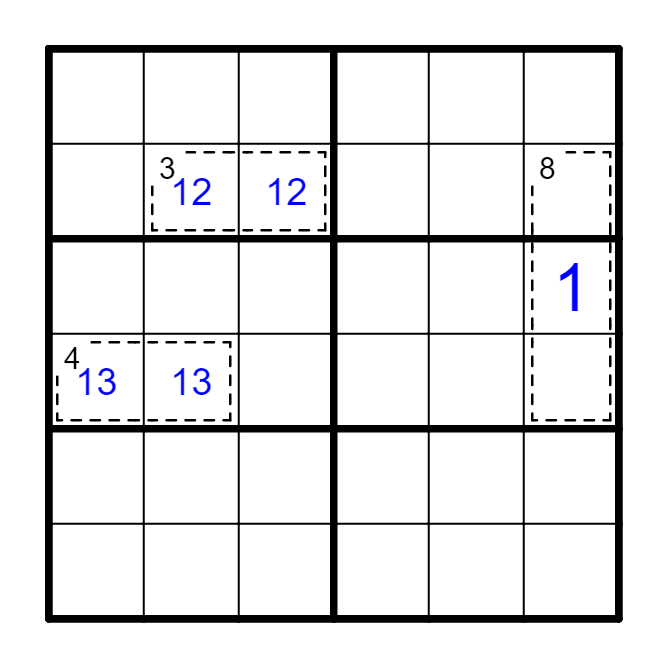
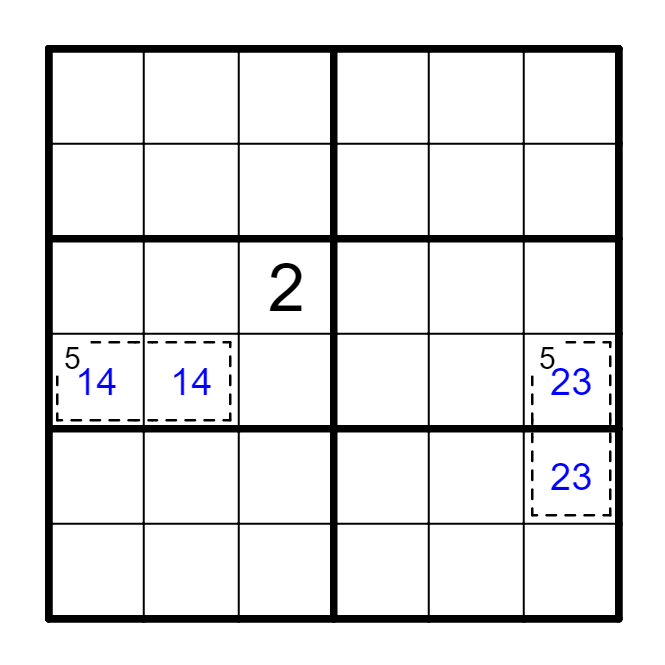
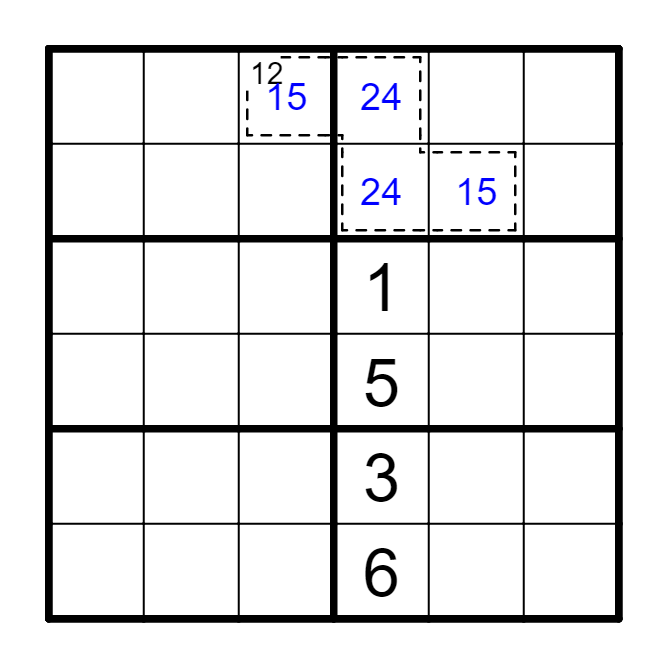
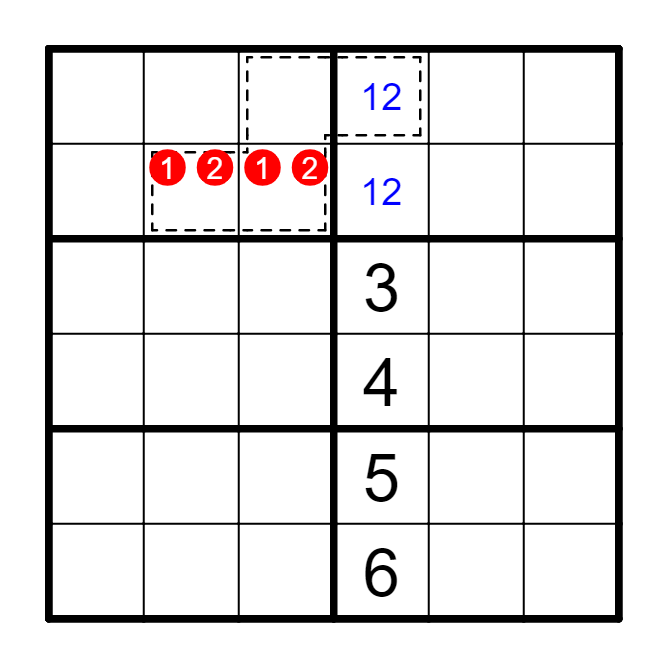
(5) 虚线框内额外区域
例 虚线框A及A6格构成额外区域。
例 整个虚线框是额外区域;若虚线框形如黄色部分所示,此处被框起的六格亦是额外区域。
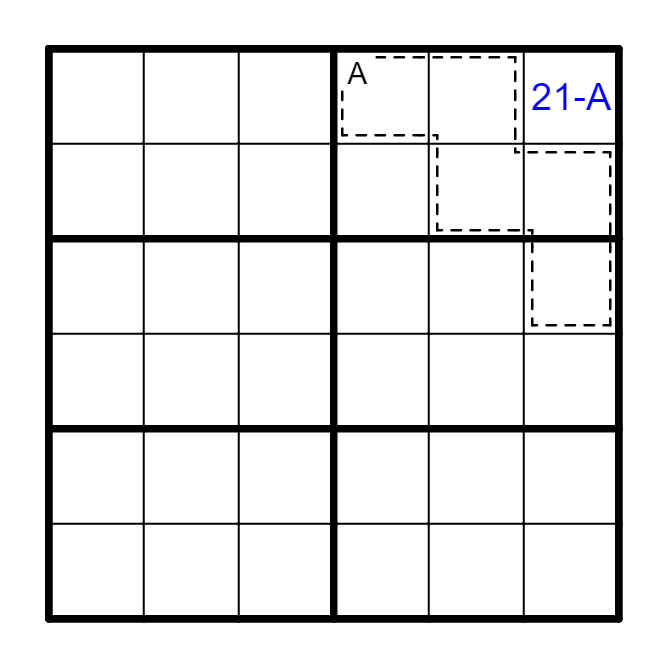
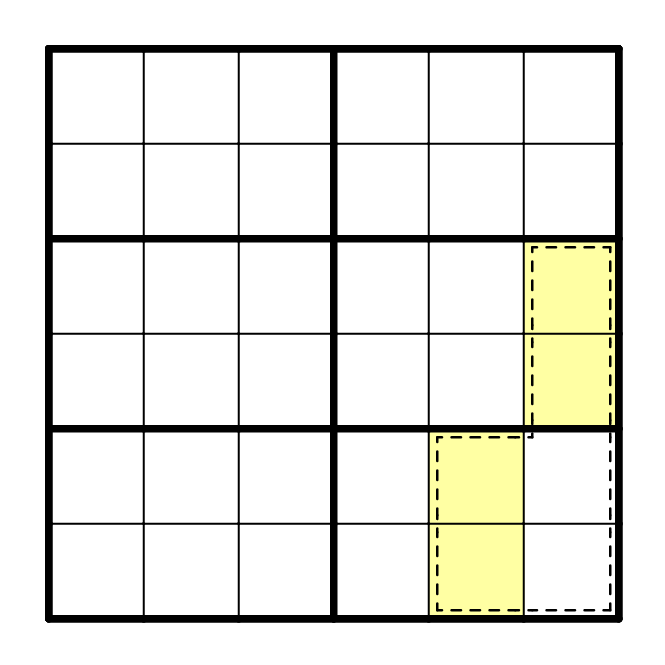
带有斜向虚线框的杀手也被称为刺客。
(6) 同数双框数对/组。
非常特殊,一般出现在两个垂直的、有相同和、双拆分的虚线框遇到时。