无马 Anti Knight

无马数独是一种全盘限制类的题目，它看起来像是标准数独。

Anti Knight is a variant with all-grid limitted. It looks like Classic.

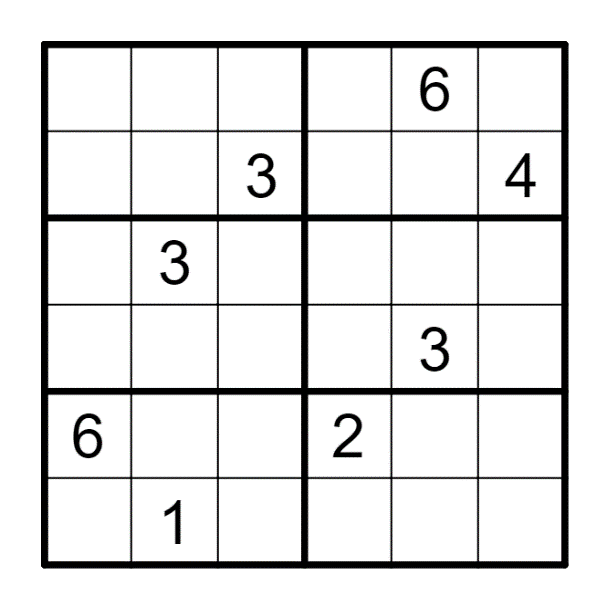
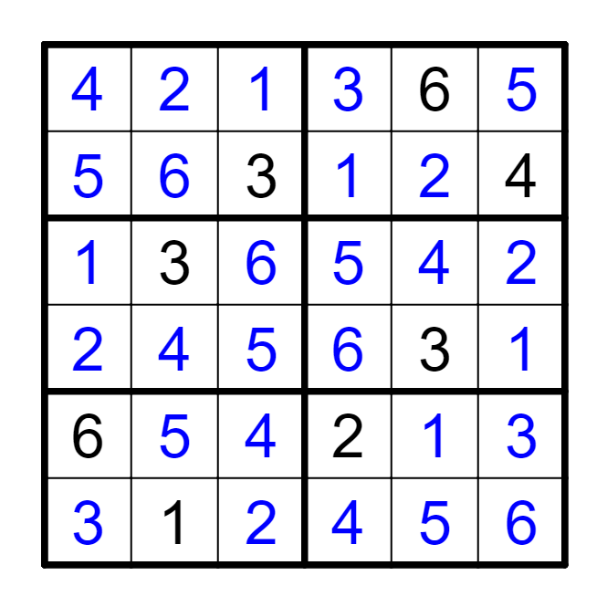
标准数独基础上，如果一格是A，从这个格起走一步马步能到的单元格内不能是A。下图展示了当C3=A时，诸如A2或B5这样的格子不能是A。

Classic rules applied. Additionally, if a cell is A, cells have Knight Step with this cell cannot be A. The next picture shows cells like A2 or B5 cannot be A when C3=A.

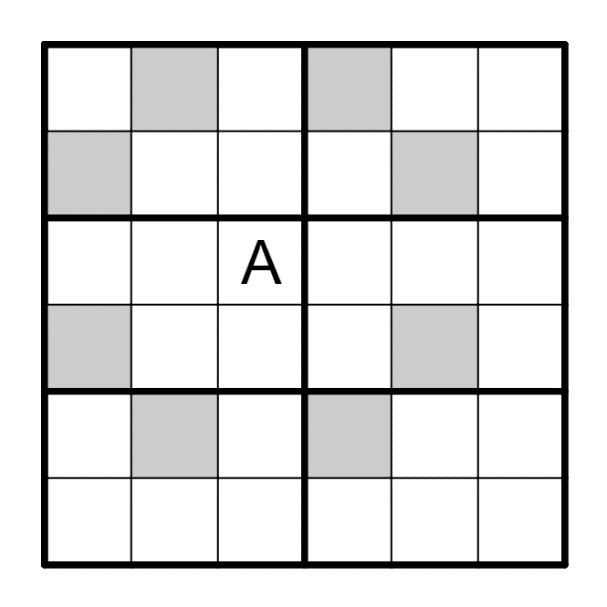
马步是象棋步法的一种，所以无马数独是一种无国际象棋类变型（无缘也是其中一种，它也被称为无王数独）。

Knight Step is one of the Chess Step, so Anti Knight is a kind of the Anti Chess variants (Untouch is another kind of them, which is also called Anti King).

◆和无缘数独类似，特殊的区块和删减非常常见。但无马数独中，特殊区块的删减域更广，因为马步经常比国王步更远一些。

Similar to Untouch, special Blocks and deletings are common. But deletings own wider domain in Anti Knight, for Knight Steps  are usually further than King Steps.

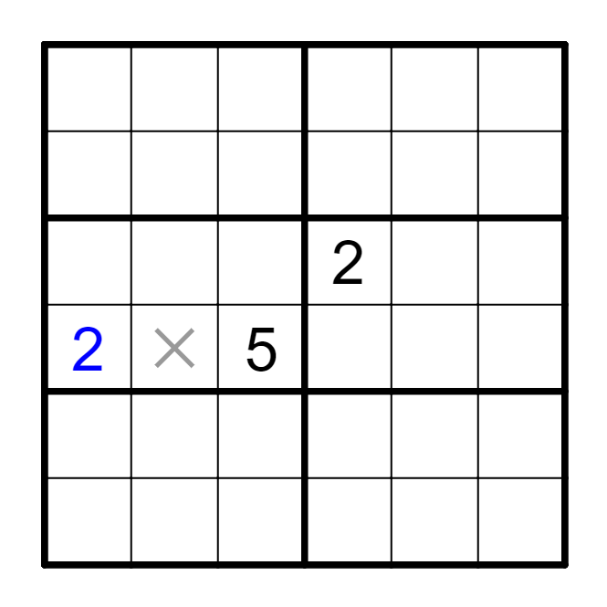
◆六阶潜规则Hidden Rules in 6x6

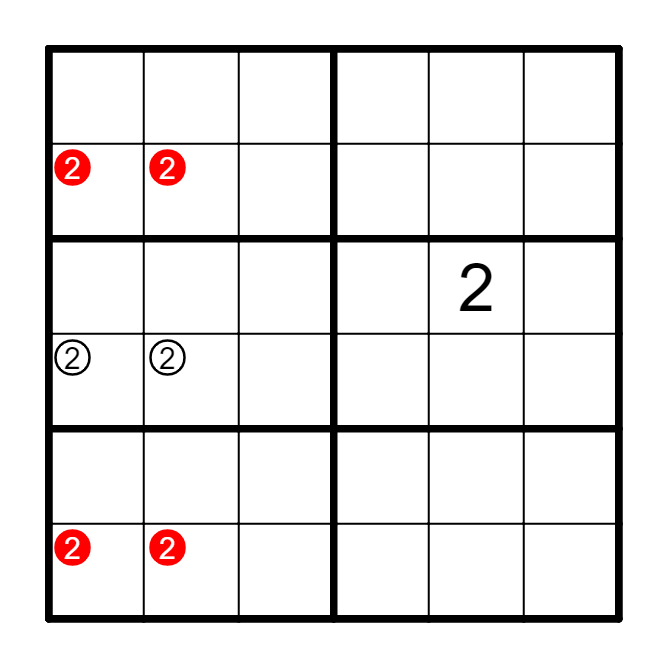
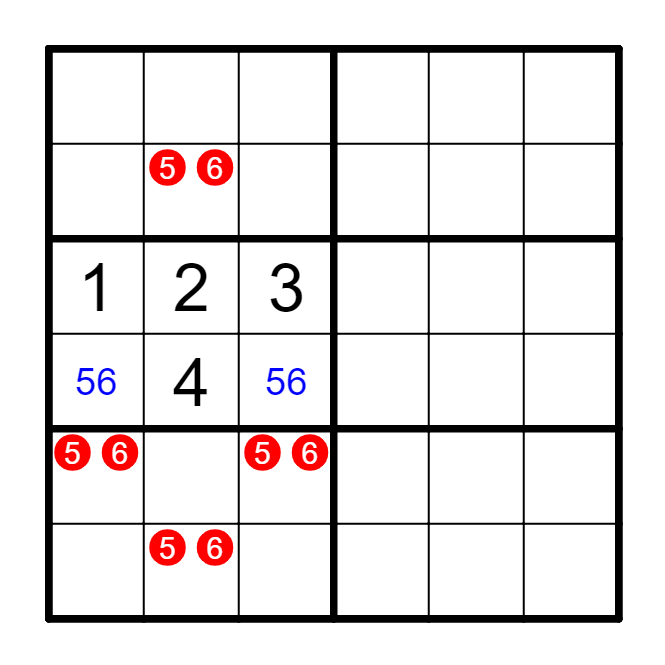
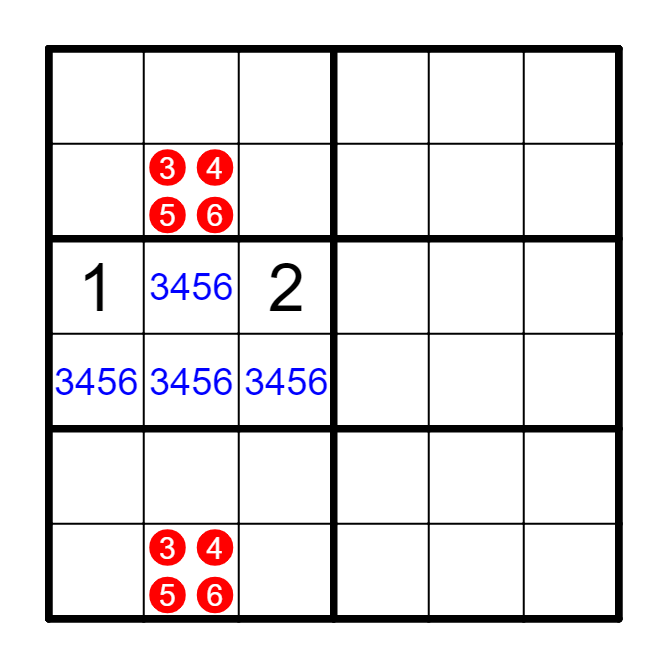
① 涂色区域有三种数字，白色区域有另外三种数字。

In 6x6 puzzles, 3 kinds of numbers in colored cells, 3 kinds of numbers in other cells.

② 符合同位数独规则。Disjoint rules are obeyed.

◆九阶潜规则 Hidden Rules in 9x9

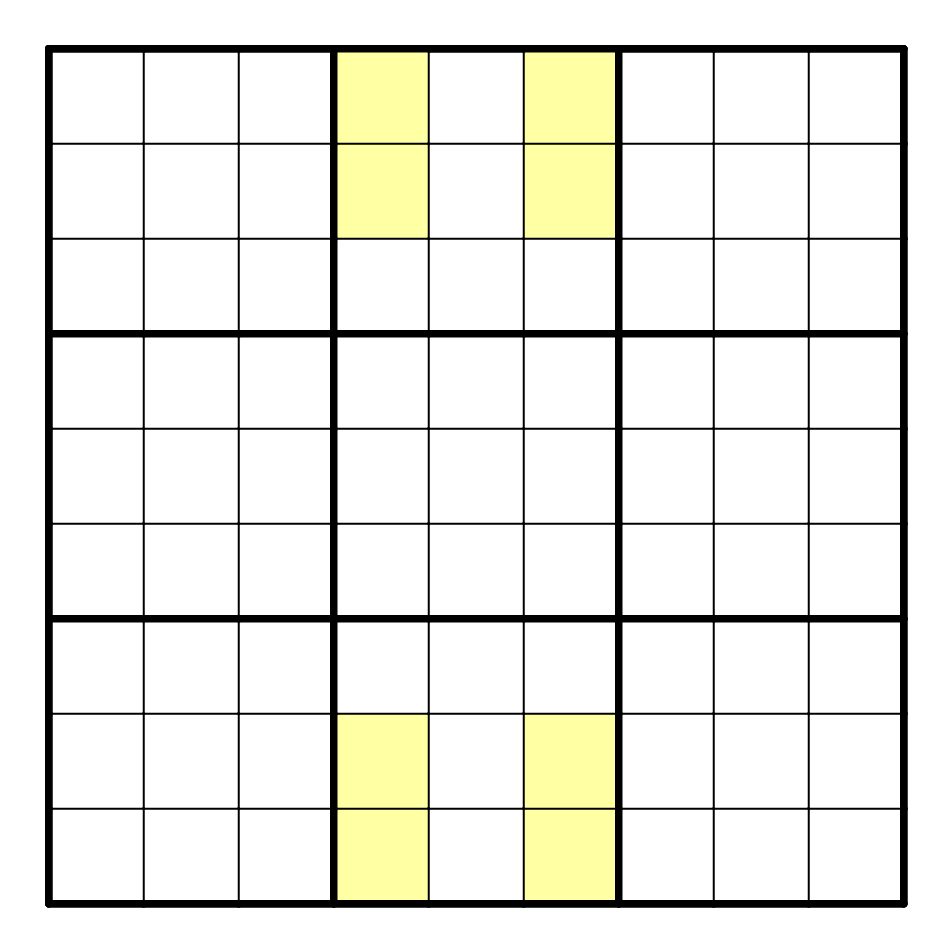
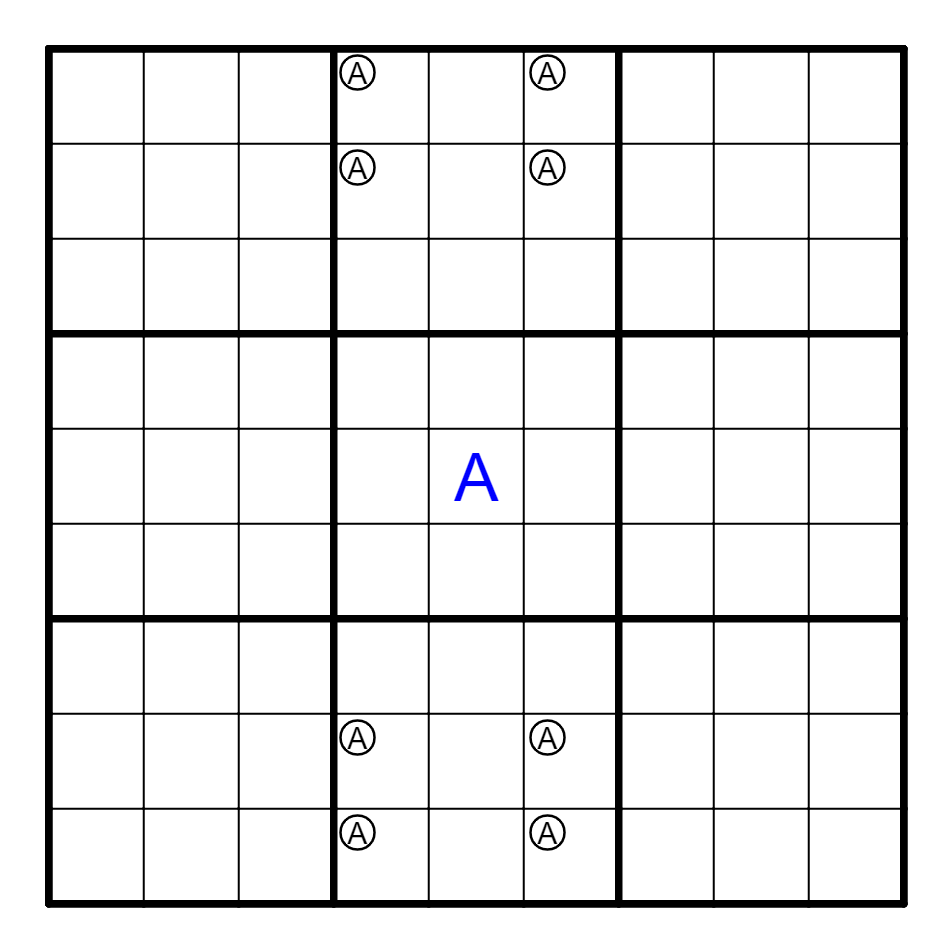
① 如果图中8格只有1个重复数字A，那么E5=A. 

If 8 cells like the yellow structure have just one repeated number A, then E5=A.

证明：如果E5=X，那么X必须在黄色区域中出现两次。

Proof: If E5=X, X must appear twice in yellow cells.

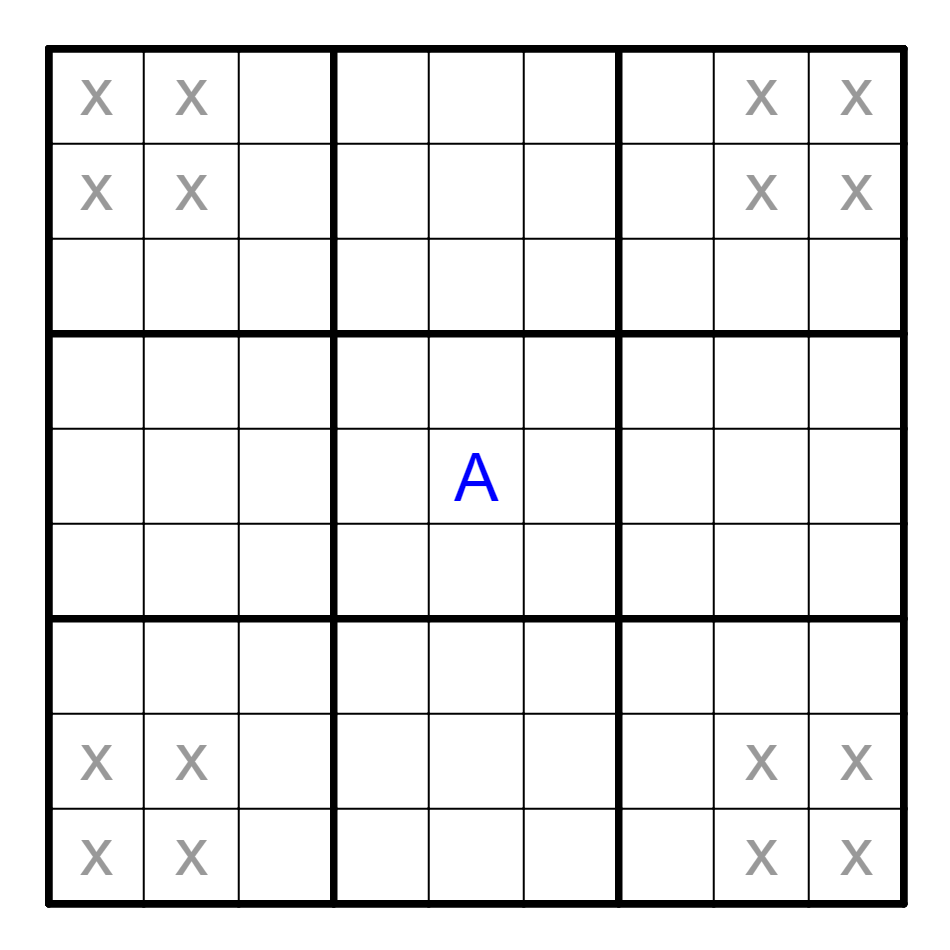
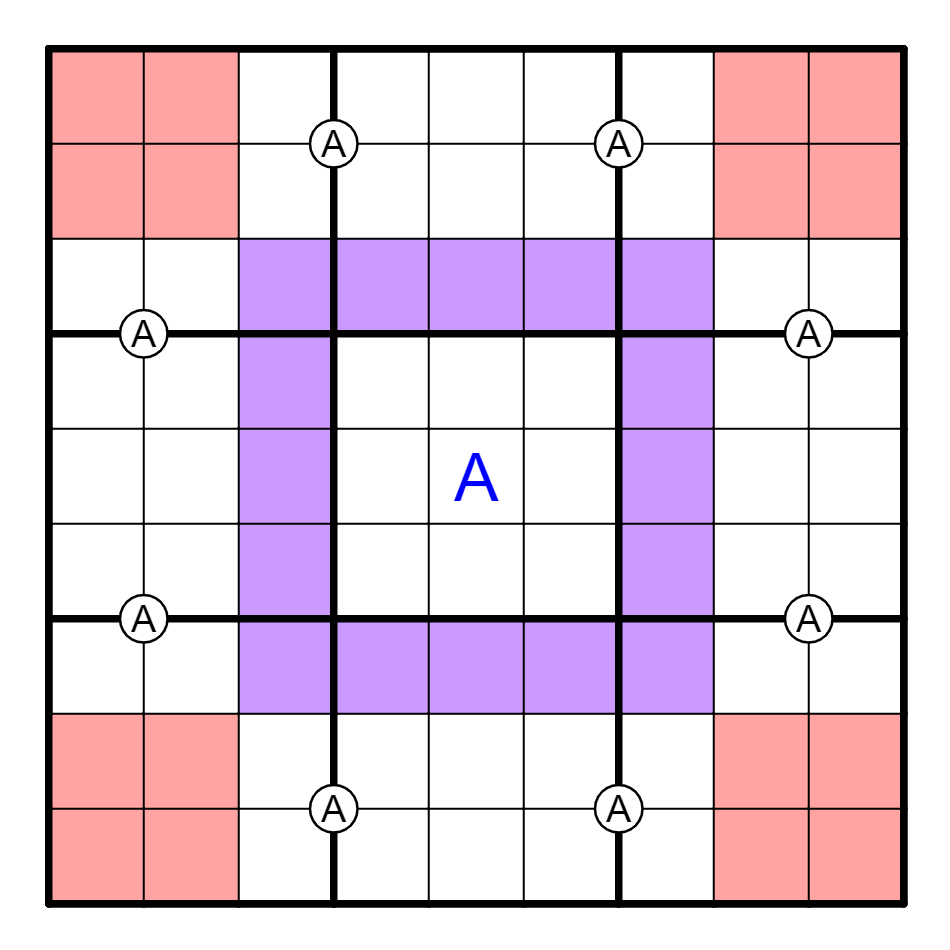
② 如果四角上这四组2x2方格都不是A，那么E5=A。

If these four 2x2 squares on corner cannot be A, then E5=A.

证明：红色区域没有A意味着紫色区域也没有A（利用互补）。但A必须出现9次，所以每个2x5的区域里有两个A，剩下E5=A。

Proof: Red cells cannot own A means purple cells cannot own A either (by complementariness). But A must be on the grid for 9 times, so each 2x5 part contains 2 A, and E5=A.

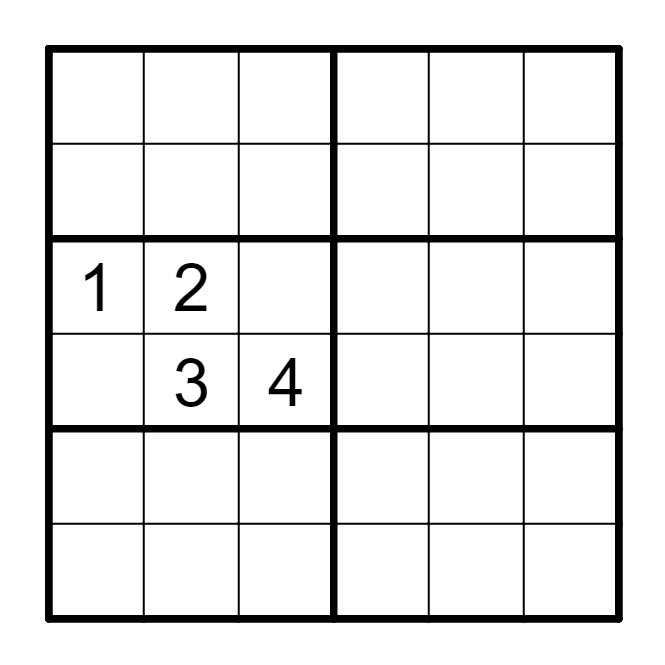
练习 Practice

① 六阶无马数独中，B2有多少个马步格？

How many cell has a Knight Step with B2 in Anti Knight 6x6?

② 哪些格不能是5或6？Which cells cannot be 5 or 6?

答案 Answer

① 4 ② B1, D5, E3