ALS

定义1 ALS

一个区域内有K个不同的单元格，和K+1种候选数，且候选数A、B各自只出现一次，那么A和B构成强链。这样的强链A==B被称为强ALS，一般称为ALS。

例 ALS

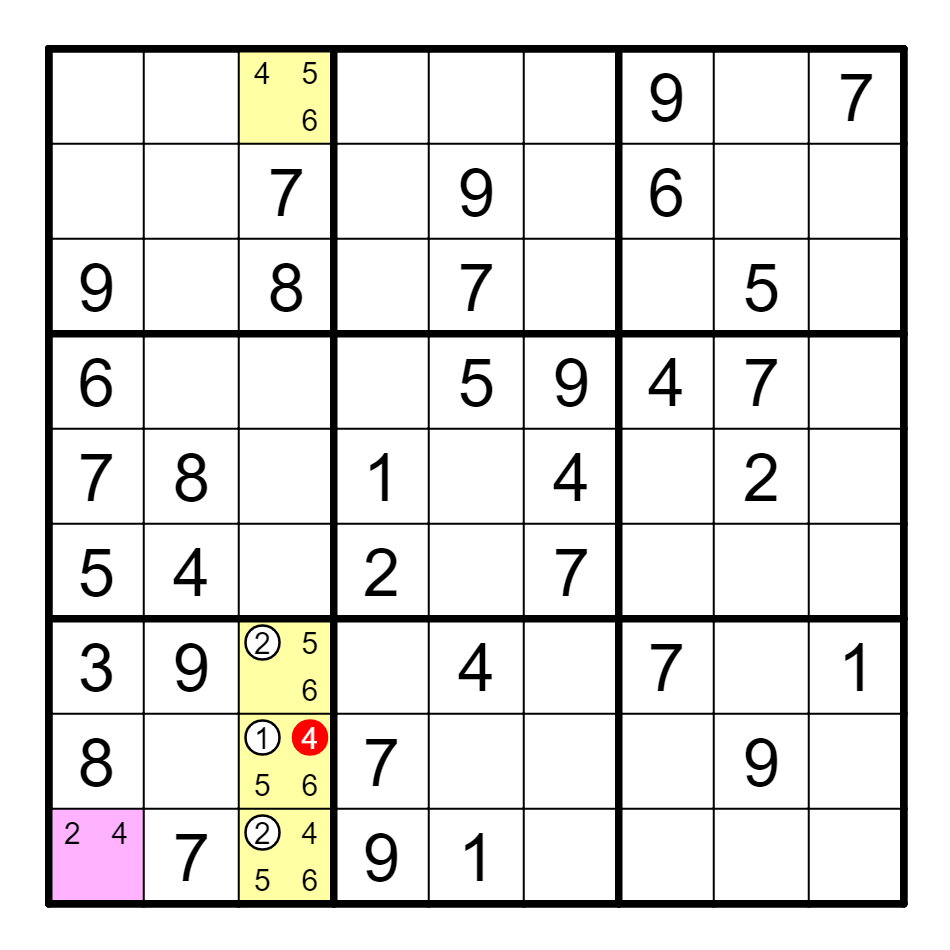
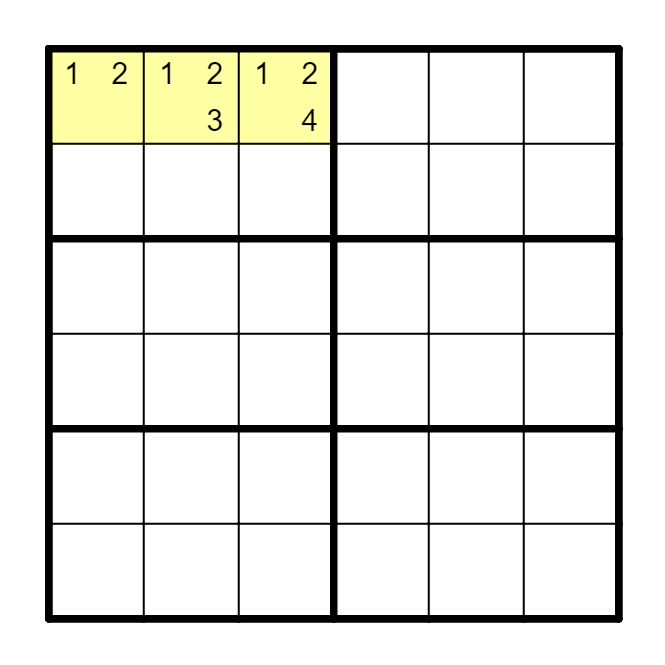
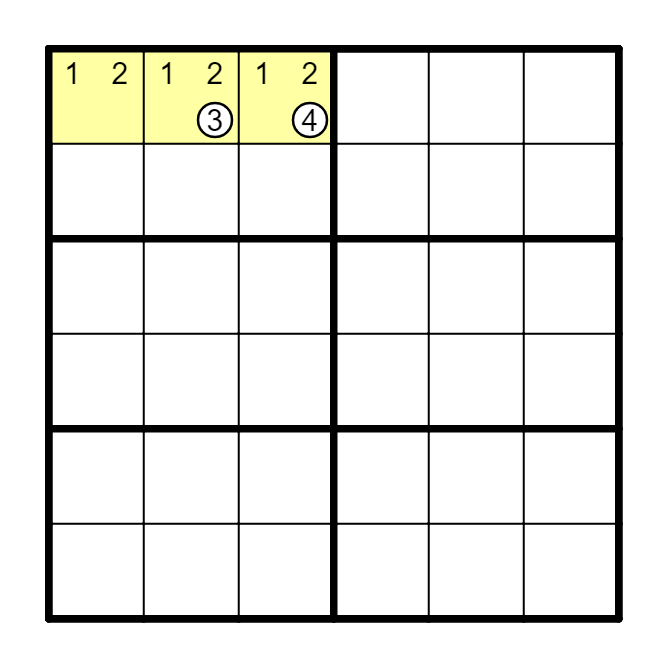
A1、A2及A3构成ALS，A2(3)==A3(4)。

定义2 ALS-XZ

两条连结的ALS链构成ALS-XZ。

① 基础ALS-XZ

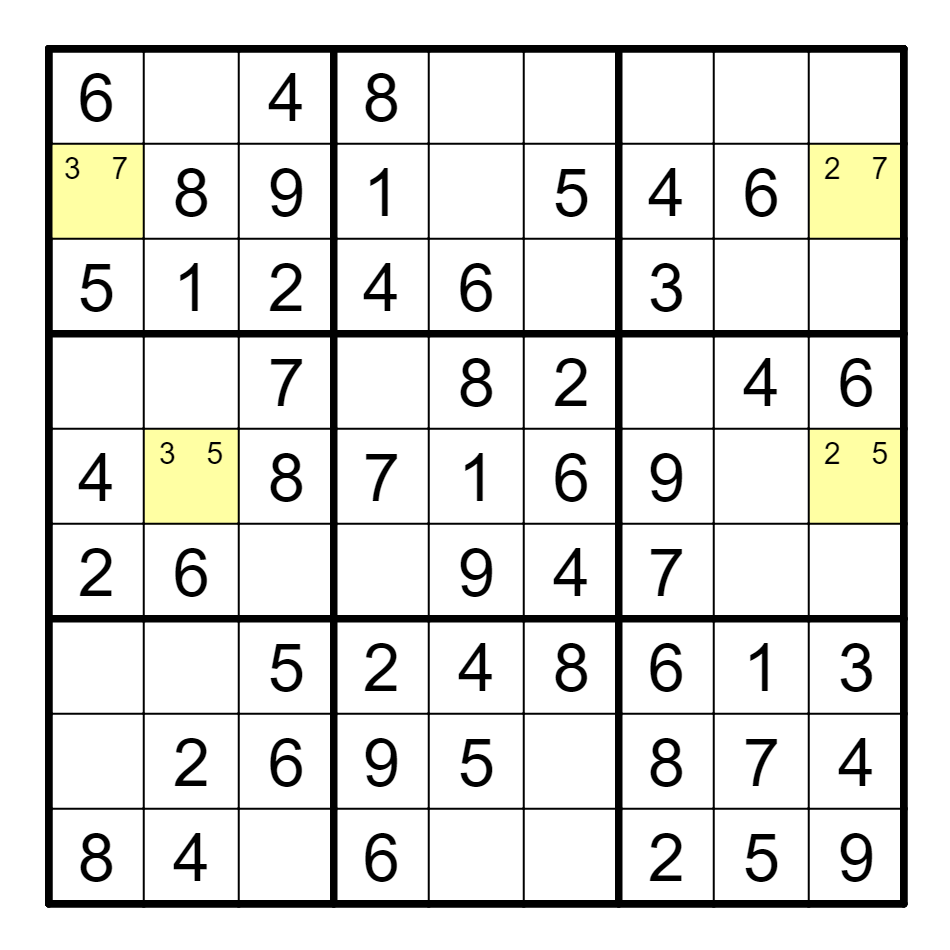
B1(3)==B9(2)--D9(2)==D2(3)，删除A2和D1的3。

② 自噬ALS-XZ（AIC）

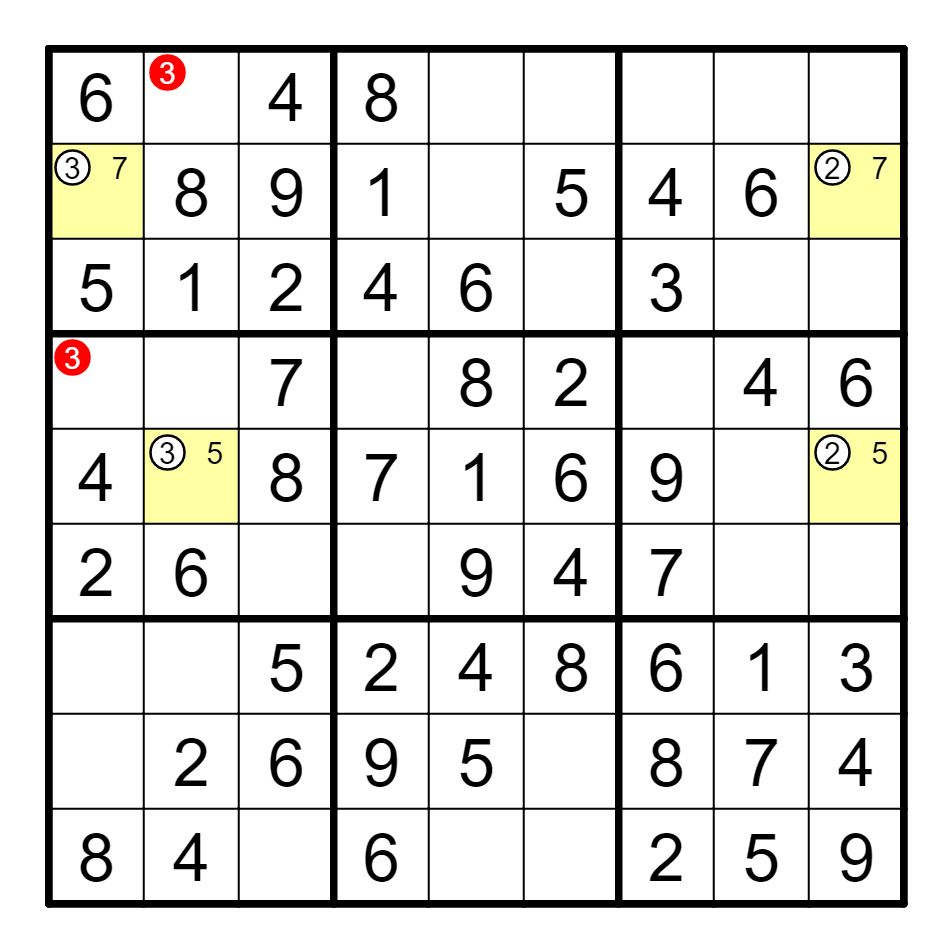
A7(3)==A2(2)--I2(2)==I7(6)，删除A7的6。这种结构删除了其本身的构成单元格，称为自噬。

③ 单格ALS-XZ

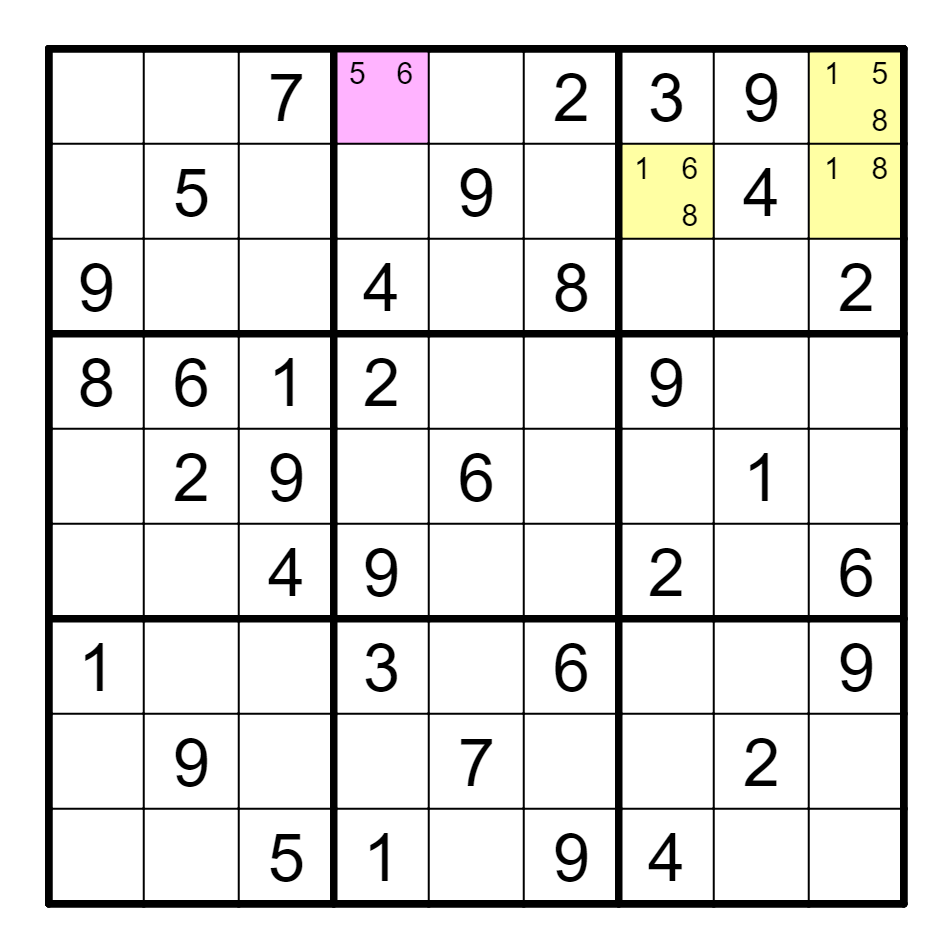
A4(6)==A4(5)--A9(5)==B7(6)，删B4的6。

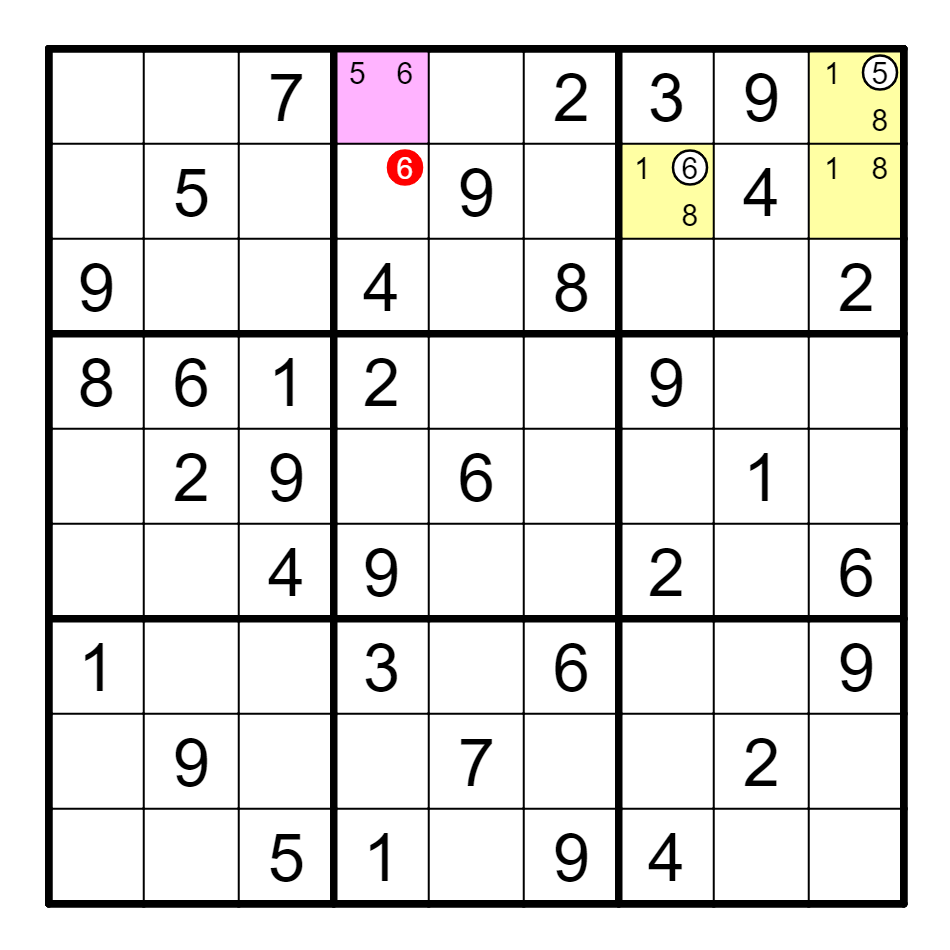
④ 带强链ALS

C2(1)==C4(8)--F4(8)==F3(1)，删A3及E2的1；

C2(1)--H2(1)==H1(1)将强链进行了传递，删E1的1。

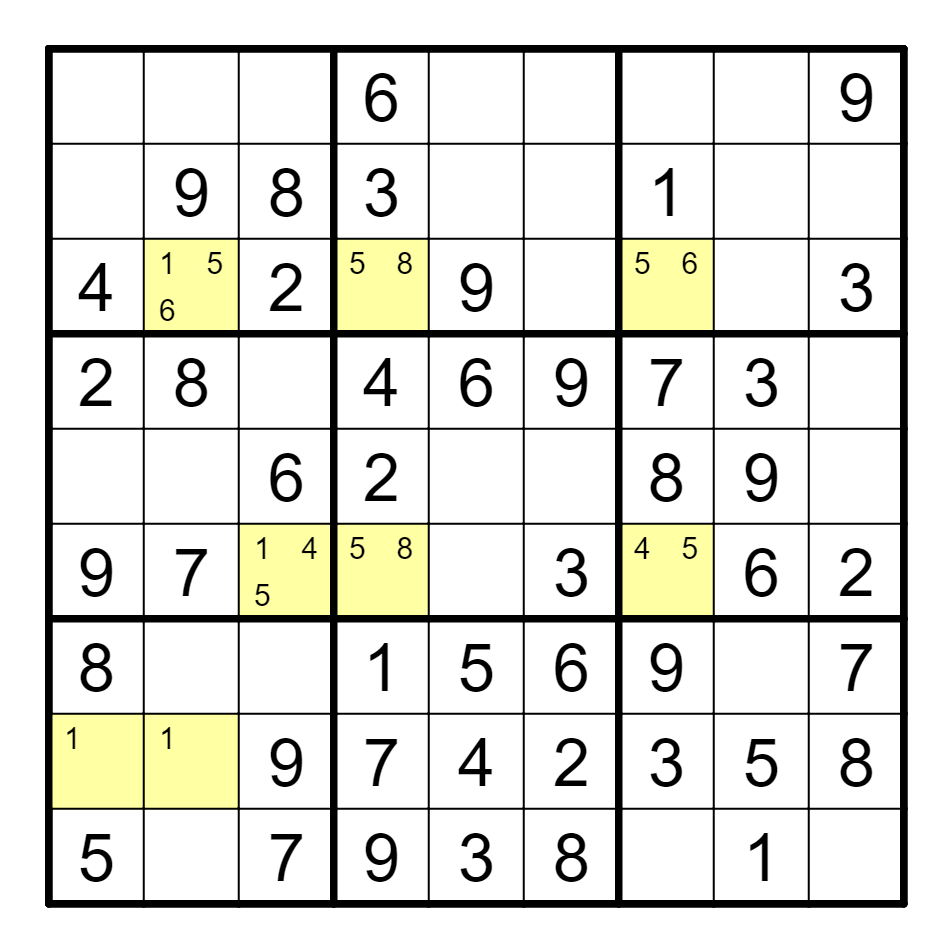
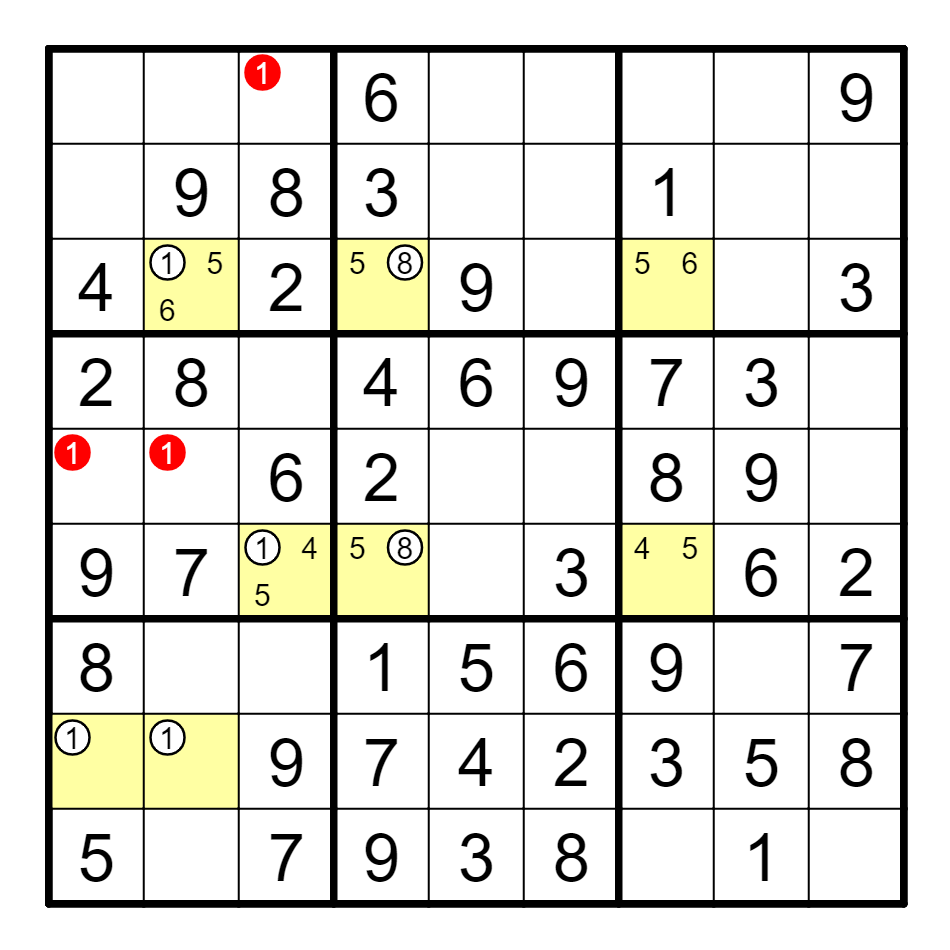
定义3 区块ALS-XZ

在一个ALS内，所有的候选数A的集合，与所有候选数B的集合，构成强链。带这样的链的ALS-XZ被称为区块ALS-XZ。

① 单组合

例 {A7, A9}(2)==A3(5)--G3(5)==G9(2)，删C9的2。

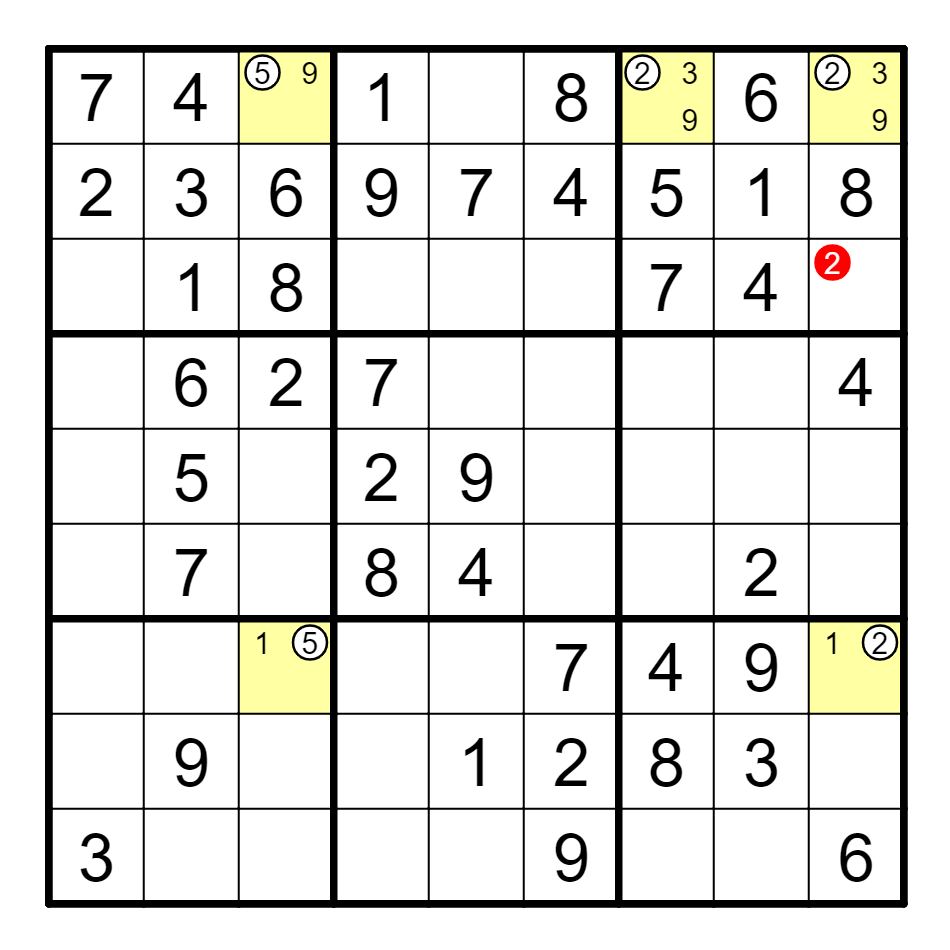
例 A6(8)==B4(6)--{G4, I4}(6)==G4(8)，删G6, H6的8。

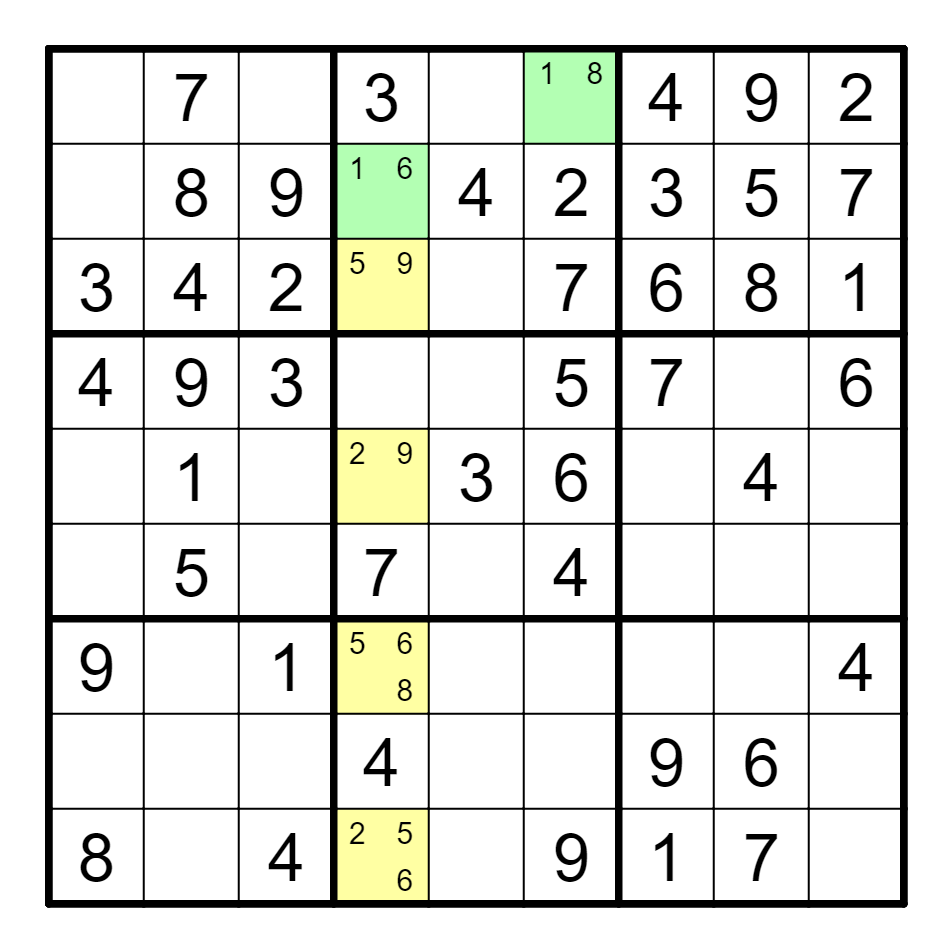
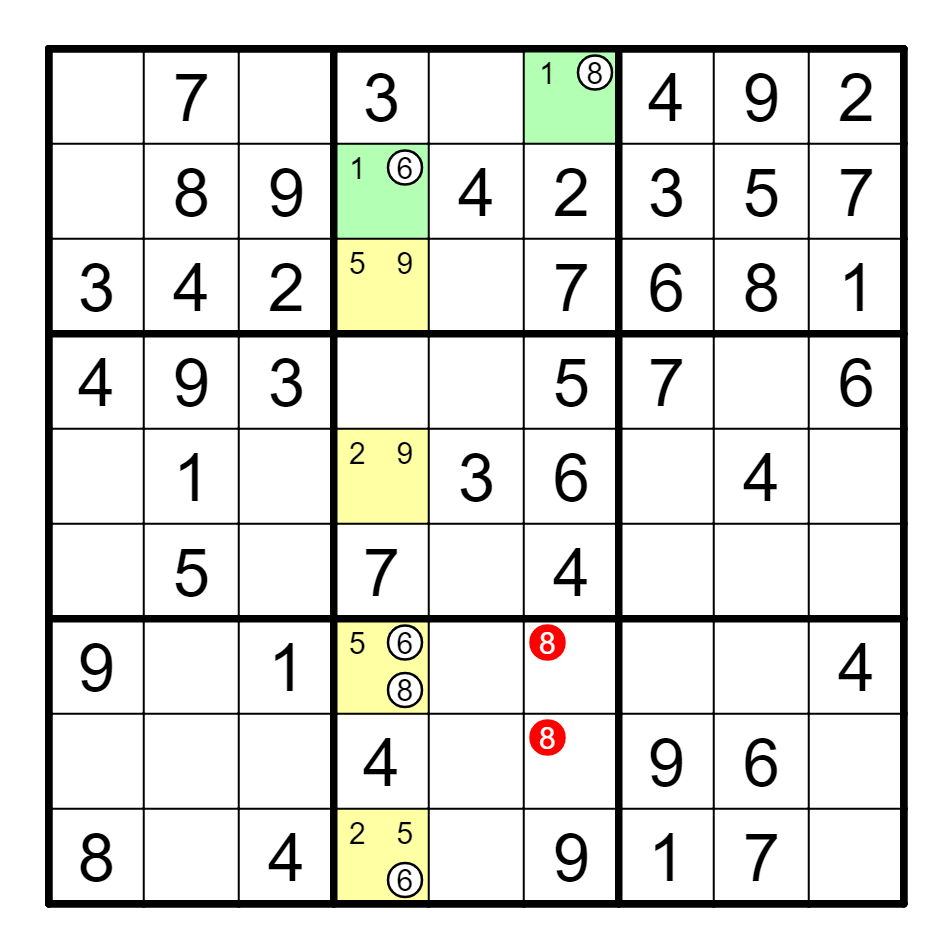
② 多组合

A8(7)=={A7, A9}(6)--B9(6)=={B4, B5}(7)，删A5的7。

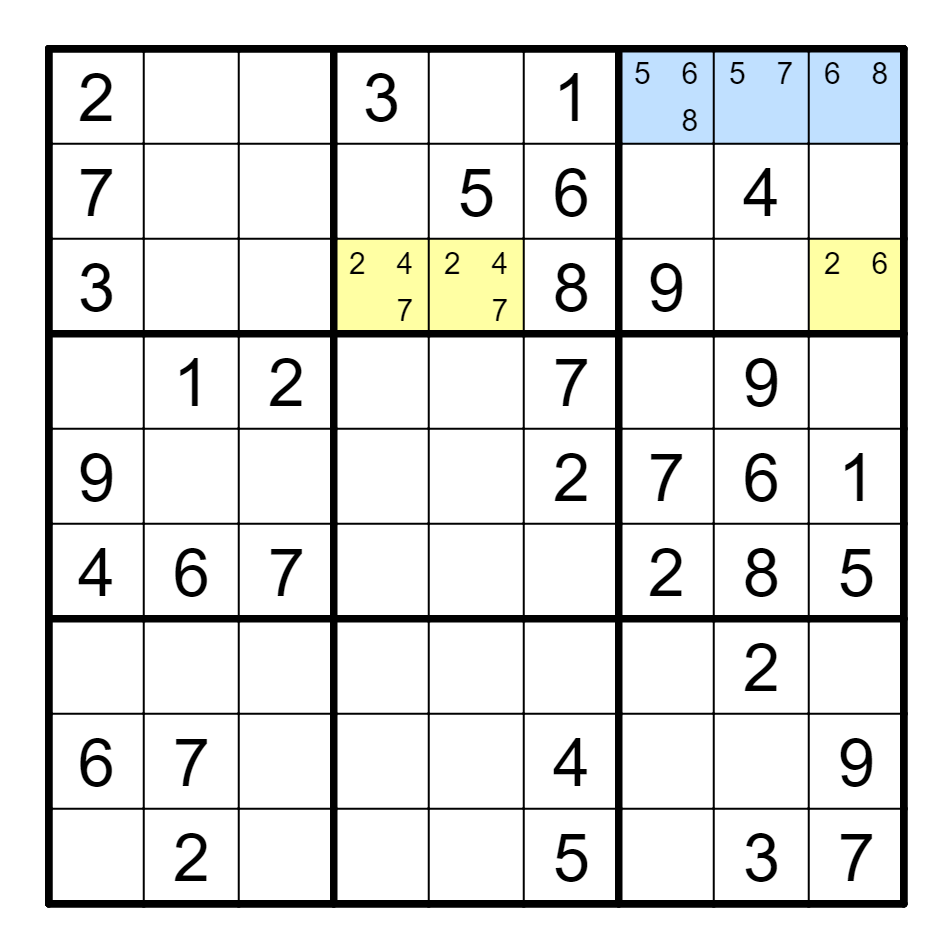
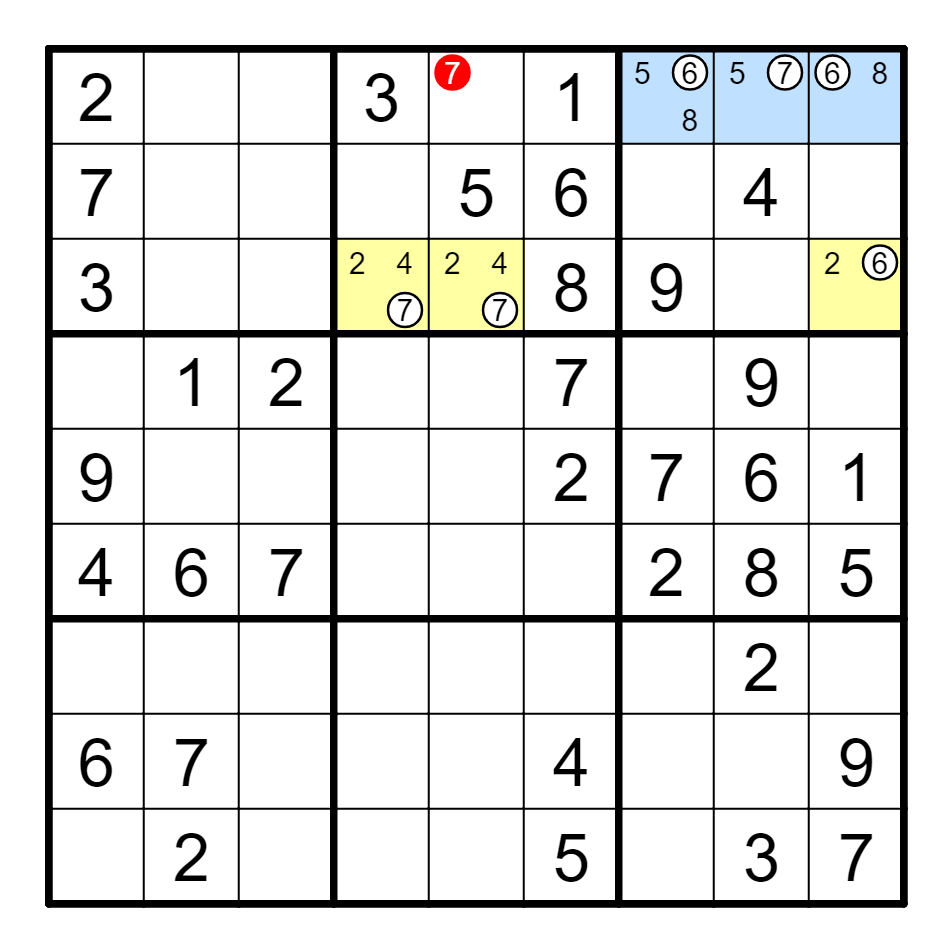
定义4 ALS不连续环

不连续环可能由ALS组成。

以下两个案例讨论了双ALS环。

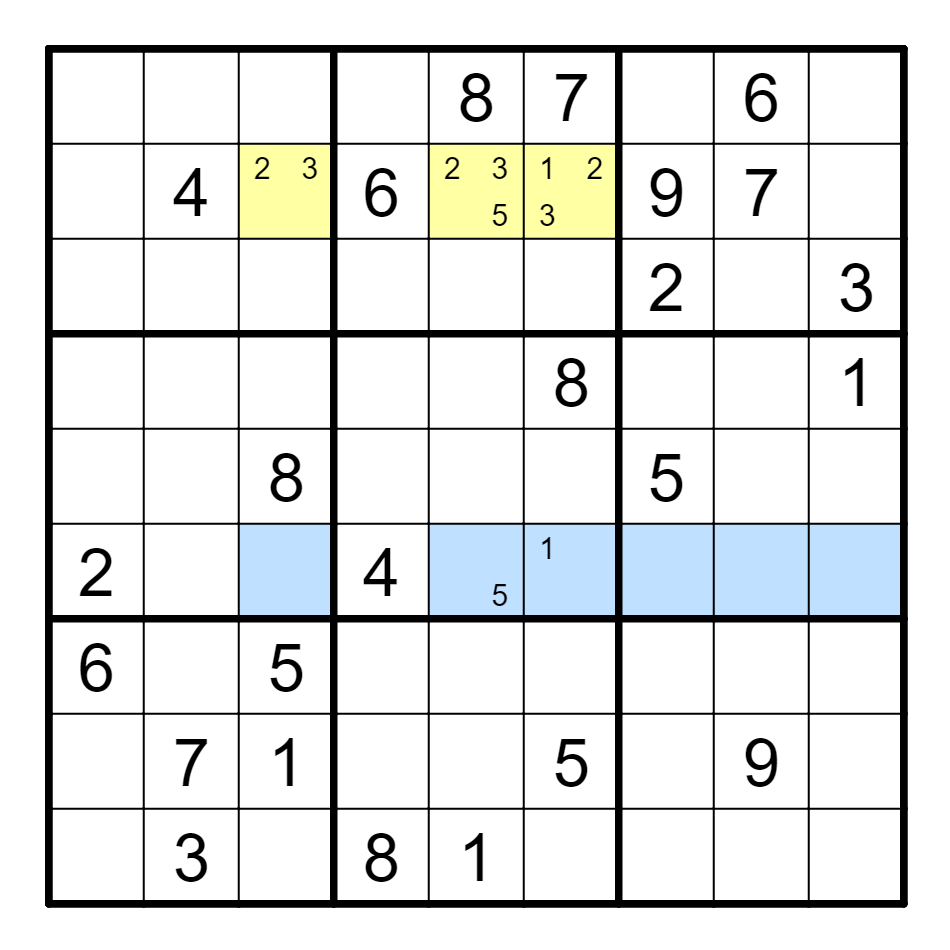
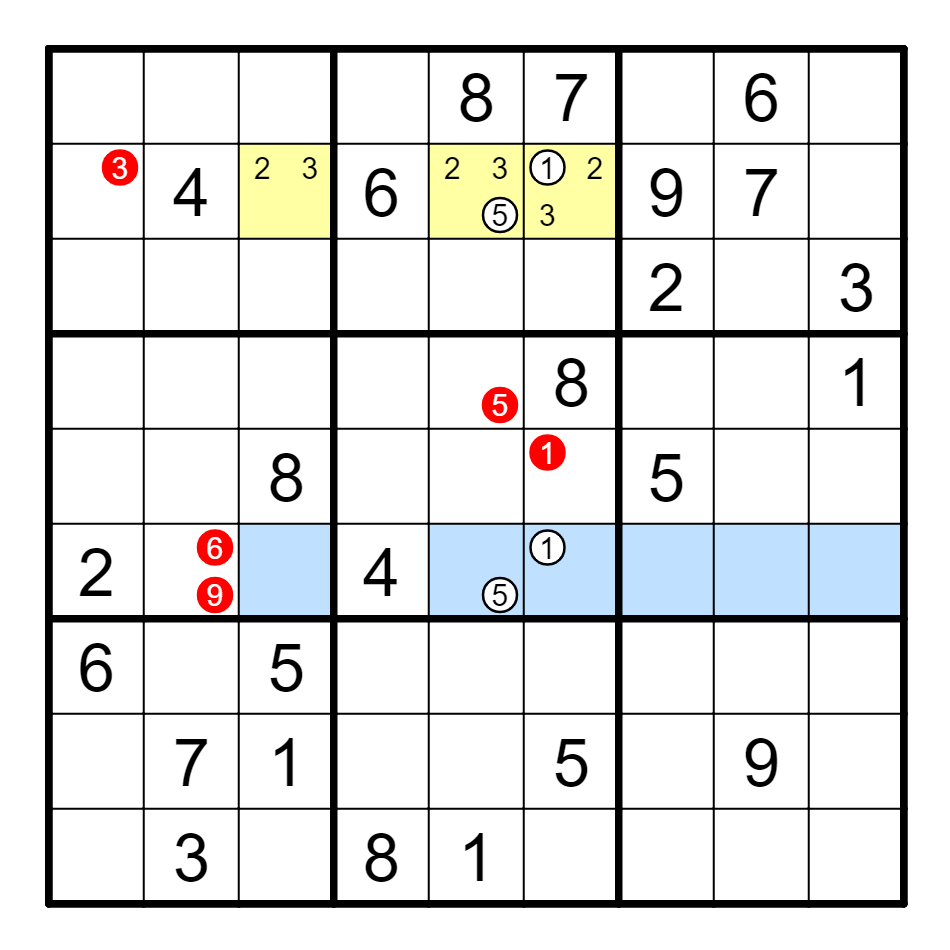
例 B5(5)==B6(1)--F6(1)==F5(5)--B5(5)，删E6的1及D5的5。

B5(5)--B6(1)，删B1的3，同理删F2的6和9。

Puzzle Author: TTH

练习

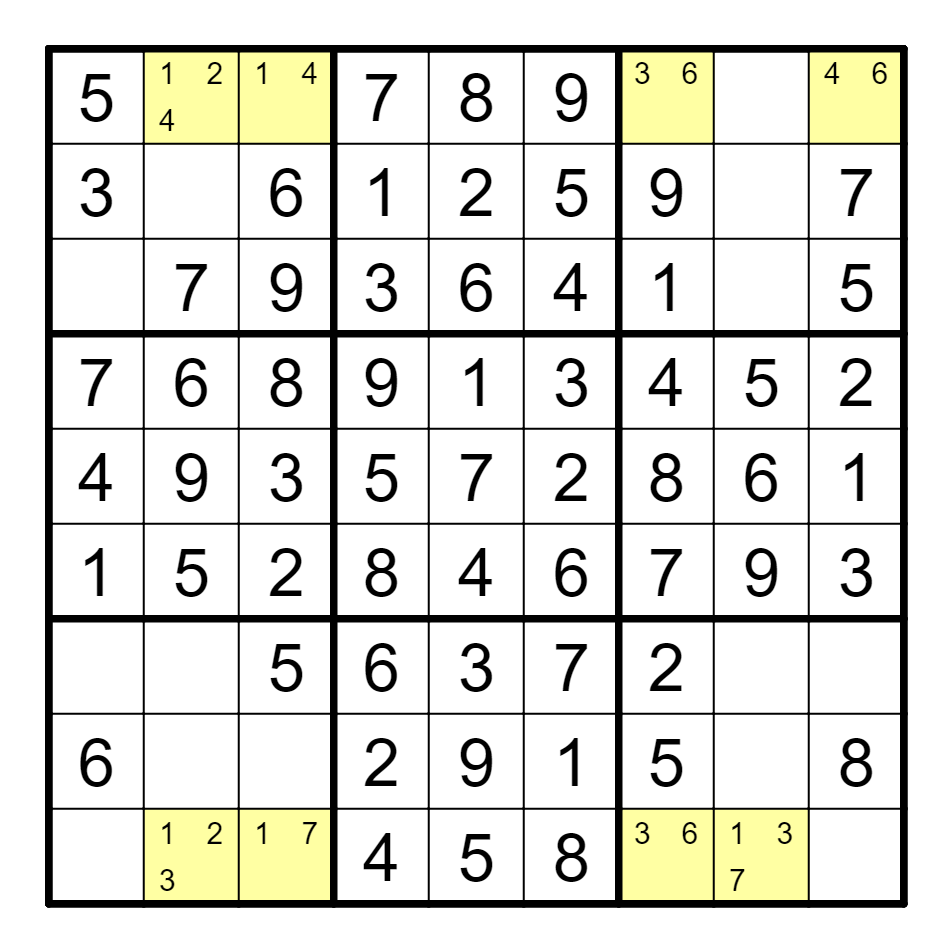
① 在涂色格中找出ALS-XZ。

(a) 用链描述这个ALS。

(b) 指出它可以删减的数字。

(c) 讨论它的类型。

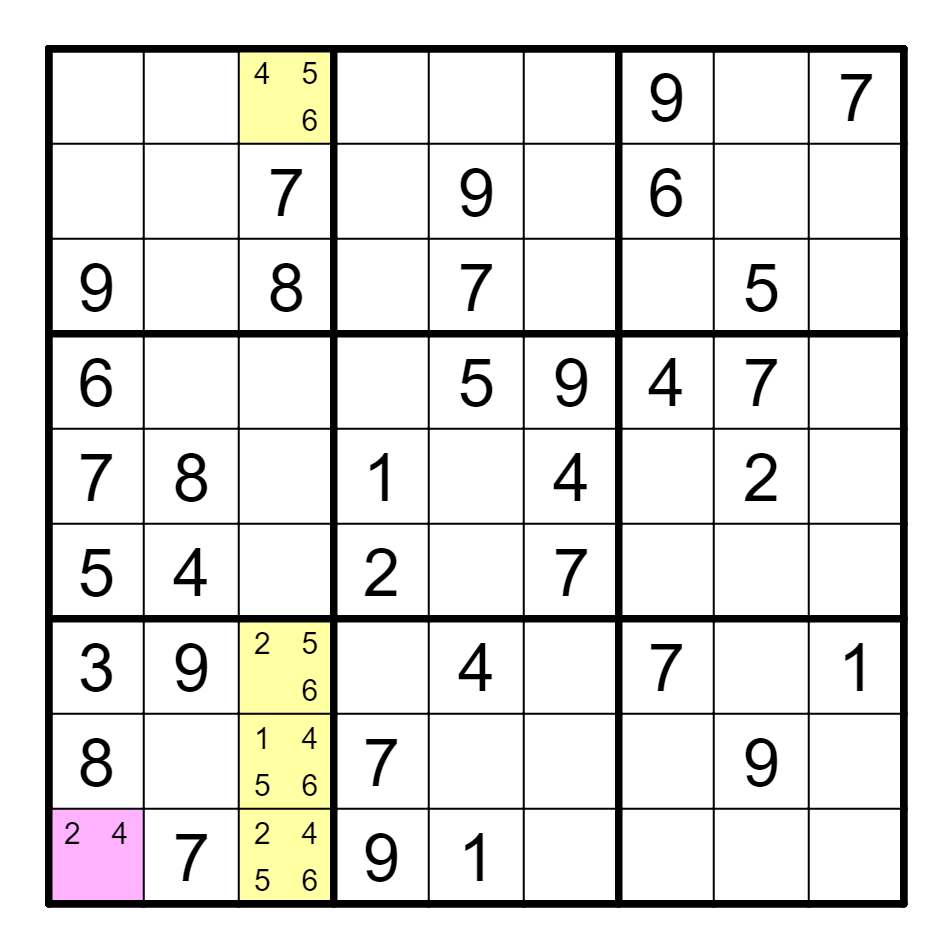
答案 Answer

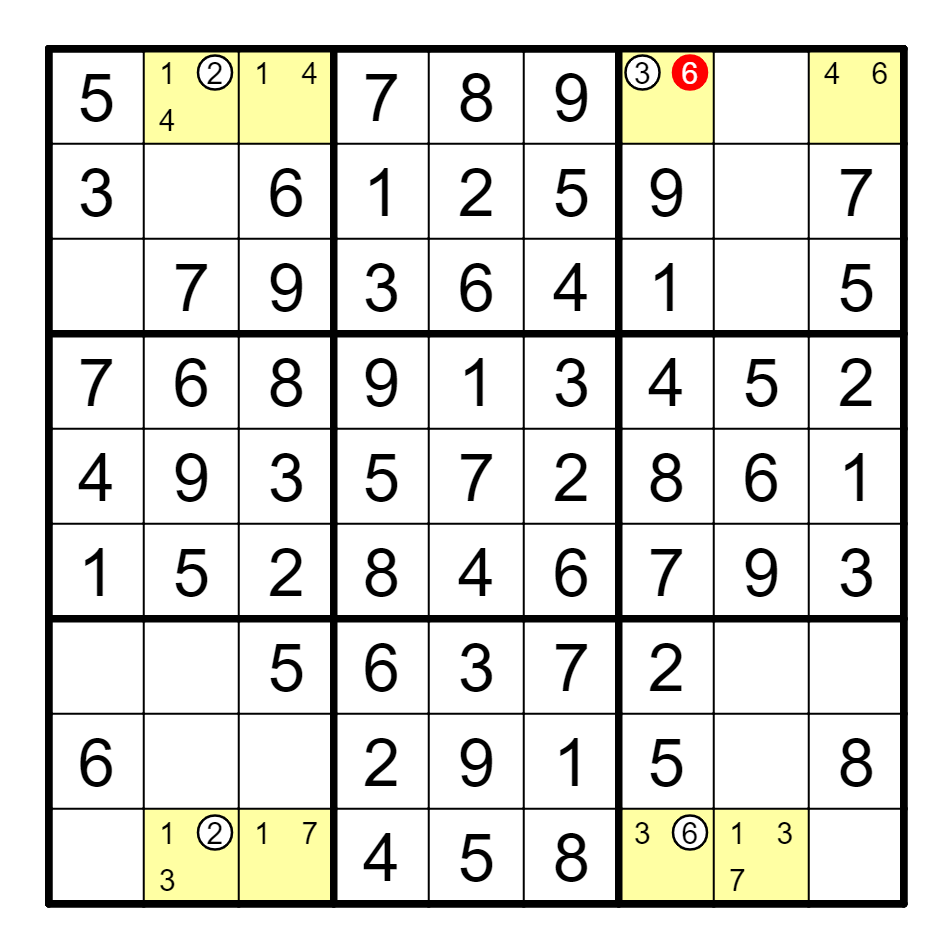
① 如图所示。

(a) H3(1)=={G3, I3}(2)--I1(2)==I1(4)

(b) 删除H3的4。

(c) 带有单格，且自噬的区块ALS-XZ。